Упражнение 592 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 171

а)  \(1{,}5;\ 2{,}5;\ 3{,}5;\ldots\); 

\(a_1 = 1{,}5;\ a_2 = 2{,}5; \ a_3 = 3{,}5\)

\(d=a_2-a_1=2,5-1,5=1.\)

\( a_4=a_3+d=3,5+1 = 4{,}5\)

\(a_5=a_4+d=4,5+1 = 5{,}5\).

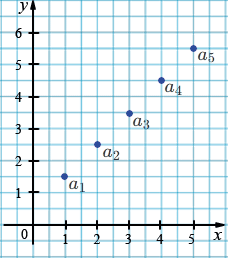
Точки на координатной плоскости:

\((1;1{,}5),\ (2;2{,}5),\ (3;3{,}5),\ (4;4{,}5),\ (5;5{,}5).\)

б) \(8;\ 4;\ 2;\ldots\)

\(b_1 = 8;\ b_2 = 4; b_3 = 2\)

\(q=\frac{b_2}{b_1}=\frac{4}{8}=\frac12\)

\( b_4 = b_3 \cdot q=2\cdot\frac12=1;\)

\(b_5 =b_4 \cdot q=1\cdot\frac12= 0{,}5\).

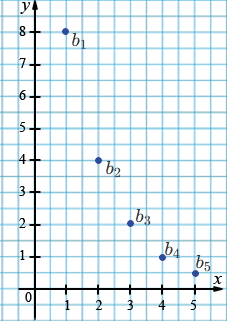
Точки на координатной плоскости: \((1;8),\ (2;4),\ (3;2),\ (4;1),\ (5;0{,}5)\).

Пояснения:

Арифметическая прогрессия — это последовательность, в которой каждый следующий член получается прибавлением к предыдущему одного и того же числа \(d\), называемого разностью прогрессии.

В пункте а) разность равна: \[ d = 2{,}5 - 1{,}5 = 1. \] Поэтому каждый следующий член увеличивается на 1, что позволяет найти первые пять членов последовательности.

Геометрическая прогрессия — это последовательность, в которой каждый следующий член получается умножением предыдущего на одно и то же число \(q\), называемое знаменателем прогрессии.

В пункте б) знаменатель равен: \[ q = \dfrac{4}{8} = \dfrac12. \] Это означает, что каждый следующий член в 2 раза меньше предыдущего.

Для изображения на координатной плоскости по оси \(x\) откладывается номер члена прогрессии, а по оси \(y\) — значение соответствующего члена. Полученные пары чисел записываются в виде координат точек.