Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии.
Определение
| Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. |
То есть последовательность \((b_n)\) - геометрическая прогрессия, если для любого натурального \(n\) выполняются условия
\(b_n\ne0\) и \(b_{n+1}=b_n\cdot q\), где \(q\) - некоторое число.
Отношение любого члена геометрической прогрессии, начиная со второго, к предыдущему члену равно \(q\), т.е. при любом натуральном \(n\) верно равенство
\(\frac{b_{n+1}}{b_n}=q.\)
Число \(q\) называют знаменателем геометрической прогрессии. Знаменатель геометрической прогрессии всегда отличен от нуля.
Чтобы найти \(b_n\), мы должны \(b_1\) умножить на \(q^{n-1}\), т.е.
\(\bold{ b_n=b_1 \cdot q^{n-1}}\) - формула \(n\) - го члена геометрической прогрессии.
Пример: зададим геометрическую прогрессию, для этого укажем ее первый член и знаменатель. Пусть \(b_1=3\) и \(q=2\), получим следующую геометрическую прогрессию:
\(3; 6; 12; 24; 48;...\)
Изображение членов прогрессии на координатной плоскости:
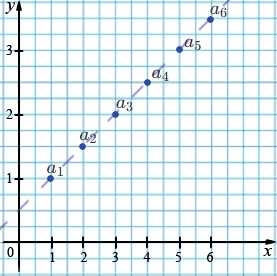
Формулу \(n\)-го члена арифметической прогрессии можно записать в виде \(a_n=dn+(a_1-d)\). Этой формулой задается линейная функция. При этом члены арифметической прогрессии будут изображаться на координатной плоскости точками с координатами \((1; a_1), (2; a_2), (3; a_3)\) и т.д. лежащими на прямой вида \(y=kx+l,\) где \(k=d, l=a_1-d.\) Изобразим на координатной плоскости первые 6 членов арифметической прогрессии
\(1; 1,5; 2; 2,5; 3; 3,5; ...\)
2. Геометрическая прогрессия.
Формулу \(n\)-го члена геометрической прогрессии можно записать в виде \(b_n=\frac{b_1}{q}\cdot q^n.\) Значит, геометрическую прогрессию можно задать формулой вида \(y=ca^x.\) Функция задаваемая данной формулой называют показательной или экспоненциальной функцией. На координатной плоскости члены геометрической прогрессии \((b_n)\) со знаменателем \(q\), где \(q>0, q\ne1,\) изображаются точками с абсциссами 1, 2, 3, ... \(n\), ..., расположенными на кривой, которая является графиком показательной функции \(y=ca^x,\) где \(c=\frac{b_1}{q}, a=q.\)
Изобразим на координатной плоскости первые 5 членов геометрической прогрессии
\(0,5; 1; 2; 4; 8; ... \).
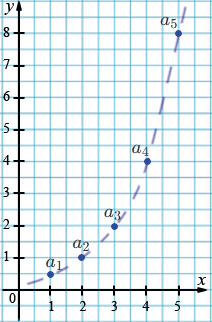
В рассмотренных случаях говорят о линейном росте членов арифметической прогрессии и об экспоненциальном росте членов геометрической прогрессии.
Свойство геометрической прогрессии:
| Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов. |
Пусть последовательность \(b_n\) является геометрической прогрессией, тогда
\(b_n=b_{n-1}q, b_{n+1}=b_nq.\)
Все члены геометрической прогрессии отличны от нуля, поэтому мы можем записать, что
\(\frac{b_n}{b_{n-1}}=\frac{b_{n+1}}{b_n},\) откуда получаем
\(\bold {b_n^2=b_{n-1}\cdot b_{n+1}}.\)
Верно и обратное утверждении:
| Если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность является геометрической прогрессией. |
Обратите внимание, что из равенства \(b_n^2=b_{n-1}\cdot b_{n+1},\) следует, что \(|b_n|=\sqrt{b_{n-1}\cdot b_{n+1}}.\) Таким образом, модуль любого члена геометрической прогрессии, начиная со второго, является средним геометрическим предыдущего и последующего членов.
Советуем посмотреть:
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии
Формула суммы первых n членов арифметической прогрессии
Формула суммы первых n членов геометрической прогрессии.
Правило встречается в следующих упражнениях:
9 класс