Упражнение 61 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 19

а) \( \dfrac{25}{x}=2x-5 \)

\(y = \dfrac{25}{x}\) - гипербола, в \(I\) и \(III\) координатных четвертях.

\(y = 2x-5 \) - возрастающая прямая, которая пересекает ось \(y\) ниже оси \(x\).

Ответ: два решения.

б) \( x^{3} = |x| \)

\(y = x^{3}\) - кубическая парабола, в \(I\) и \(III\) координатных четвертях.

\(у = |x| \) - функция модуля, в \(I\) и \(II\) координатных четвертях.

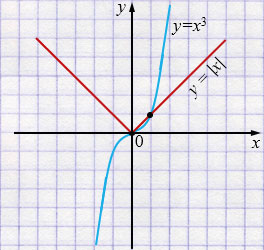
Ответ: два решения.

Пояснения:

Чтобы определить, сколько решений имеет уравнение, используем графический способ. Строим графики функций, стоящих в левой и правой частях уравнения и находим их точки пересечения. Количество точек пересечения соответствует количеству решений уравнения.