Упражнение 14 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 10

\(\sqrt{7} \approx 2{,}65\);

\(-\sqrt{11} \approx -3{,}32\);

\(\sqrt{12{,}3} \approx 3{,}51\);

\(\dfrac{12}{13} \approx 0{,}92\);

\(\dfrac{1}{2} = 0{,}5\);

\(3\dfrac{1}{3} = \dfrac{10}{3} \approx 3{,}33\);

\(0\);

\(1{,}6+\sqrt{2} \approx 1{,}6+1{,}41 \approx 3{,}01\).

\(-\sqrt{11}< 0< \dfrac{1}{2}< \dfrac{12}{13}<\sqrt{7}<\)

\(<1{,}6+\sqrt{2}<3\dfrac{1}{3}< \sqrt{12{,}3}.\)

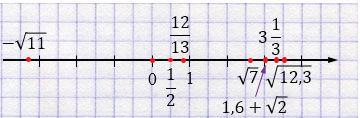
Пояснения:

Точки на координатной прямой соответствуют действительным числам: чем число меньше, тем левее точка, чем больше — тем правее.

1. Приближённые значения корней и сложных выражений.

Чтобы расположить числа на оси, удобно заменить иррациональные числа их десятичными приближениями:

\( \sqrt{7} \approx 2{,}65,\quad \sqrt{11} \approx 3{,}32,\)

\(\sqrt{12{,}3} \approx 3{,}51,\quad \sqrt{2} \approx 1{,}41. \)

Тогда: \[ 1{,}6+\sqrt{2} \approx 1{,}6+1{,}41 = 3{,}01. \]

2. Преобразование дробей.

Обыкновенные дроби записываем как десятичные:

\[ \dfrac{12}{13} \approx 0{,}92,\quad \dfrac{1}{2} = 0{,}5,\quad 3\dfrac{1}{3} = \dfrac{10}{3} \approx 3{,}33. \]

3. Расположение на прямой.

Сравнивая получившиеся приближённые значения, видим:

\( -3{,}32\;(-\sqrt{11}) < 0 < 0{,}5\;(\dfrac{1}{2}) < \)

\(<0{,}92\;(\dfrac{12}{13}) < 2{,}65\;(\sqrt{7}) <\)

\(<3{,}01\;(1{,}6+\sqrt{2}) < 3{,}33\;(3\dfrac{1}{3}) <\)

\(<3{,}51\;(\sqrt{12{,}3}). \)

Именно в таком порядке нужно отметить точки на координатной прямой.