Упражнение 924 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№924 учебника 2023-2025 (стр. 206):
Используя координатную прямую, найдите пересечение промежутков:
а) \((1; 8)\) и \((5; 10)\);
б) \([-4; 4]\) и \([-6; 6]\);
в) \((5; +\infty)\) и \((7; +\infty)\);
г) \((-\infty; 10)\) и \((-\infty; 6)\).
№924 учебника 2013-2022 (стр. 207):
Сравните площадь квадрата с площадью произвольного прямоугольника, имеющего тот же периметр.
Подсказка
№924 учебника 2023-2025 (стр. 206):
Вспомните, числовые промежутки, их пересечение.
№924 учебника 2013-2022 (стр. 207):
Вспомните:
- Как найти периметр и площадь прямоугольника.
- Как найти периметр и площадь квадрата.
- Числовые неравенства.
- Свойства числовых неравенств.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Квадрат суммы и квадрат разности двух выражений.
- Противоположные выражения.
- Вычитание дробей с разными знаменателями.
- Сравнение рациональных чисел.
Ответ
№924 учебника 2023-2025 (стр. 206):
а) \((1; 8)\) и \((5; 10)\)
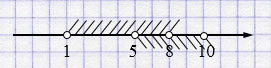
\((1; 8) \cap (5; 10) = (5; 8)\).
б) \([-4; 4]\) и \([-6; 6]\)
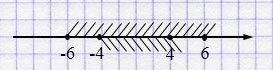
\([-4; 4] \cap [-6; 6] = [-4; 4]\).
в) \((5; +\infty)\) и \((7; +\infty)\)
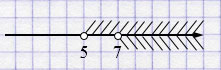
\((5; +\infty) \cap (7; +\infty) = (7; +\infty)\).
г) \((-\infty; 10)\) и \((-\infty; 6)\)
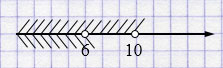
\((-\infty; 10) \cap (-\infty; 6) = (-\infty; 6)\).
Пояснения:
Пересечение двух промежутков — это множество чисел, которые принадлежат и первому, и второму промежутку одновременно.
№924 учебника 2013-2022 (стр. 207):
Пусть \(a\) и \(b\) стороны прямоугольника (\(a \neq b\)), тогда его периметр равен \(2(a + b) \), а площадь \(ab\).
Пусть \(c\) сторона квадрата, тогда его периметр равен \(4c\), а площадь \(c^2\).
Периметры прямоугольника и квадрата равны:
\(4c =2(a+b) \) \(/ : 4\)
\(c = \frac{a+b}{2}\)
\(c^2 = (\frac{a+b}{2})^2 = \frac{(a+b)^2}{4}=\)
\(= \frac{a^2 + 2ab+b^2}{4}\)
Сравним площади:
\(ab \; {\color{red}{?}} \; \frac{a^2 + 2ab+b^2}{4}\)
\(ab ^{\color{blue}{\backslash4}} - \frac{a^2 + 2ab+b^2}{4}=\)
\(= \frac{4ab - (a^2 + 2ab+b^2)}{4}=\)
\(= \frac{4ab - a^2 - 2ab-b^2}{4}=\)
\(= \frac{ -a^2 + 2ab-b^2}{4}=\)
\(= \frac{ -(a^2 - 2ab+b^2)}{4}=\)
\(= -\frac{ (a -b)^2}{4} < 0\), так как \(a \neq b\).
Ответ: площадь квадрата больше площади прямоугольника.
Пояснения:
Периметр прямоугольника равен удвоенной сумме его длины и ширины, а площадь прямоугольника равна произведению его длины и ширины.
Периметр квадрата равен длине его стороны, умноженной на 4, а площадь квадрата равна квадрату его стороны.
Обозначив стороны прямоугольника и квадрата, составляем выражения для их периметров и площадей. Учитывая то, что периметры прямоугольника и квадрата равны, выражаем сторону квадрата через стороны прямоугольника, а затем выражаем площадь квадрата через стороны прямоугольника.
Далее сравниваем площади прямоугольника и квадрата:
\(ab \; {\color{red}{?}} \; \frac{a^2 + 2ab+b^2}{4}\).
Чтобы сравнить площади, вычитаем из площади прямоугольника площадь квадрата., в результате получили выражение \( -\frac{ (a -b)^2}{4}\), которое при \(a \neq b\) меньше нуля. Следовательно, площадь квадрата больше площади прямоугольника.
Вернуться к содержанию учебника