Упражнение 479 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№479 учебника 2023-2025 (стр. 111):
Постройте график функции
\[y = \sqrt{\lvert x\rvert}.\]
№479 учебника 2013-2022 (стр. 112):
Известно, что \(a<0\) и \(b<0\). Представьте выражение:
а) \(\sqrt{ab}\) в виде произведения корней;
б) \(\displaystyle \sqrt{\frac{a}{b}}\) в виде частного корней.
Подсказка
№479 учебника 2023-2025 (стр. 111):
№479 учебника 2013-2022 (стр. 112):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Умножение рациональных чисел.
- Деление и дроби.
- Деление рациональных чисел.
- Сравнение рациональных чисел.
Ответ
№479 учебника 2023-2025 (стр. 111):
\[y = \sqrt{\lvert x\rvert}.\]
Если \(x\ge0\), то \(y=\sqrt{x}\);
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
Если \(x<0\), то \(y=\sqrt{-x}.\)
| \(x\) | 0 | -1 | -4 | -9 |
| \(y\) | 0 | 1 | 2 | 3 |
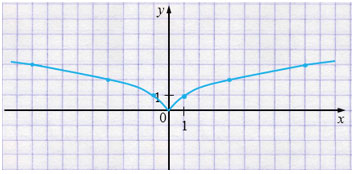
Пояснения:
Использованные приёмы и правила:
1. Определение модуля:
\(\lvert x\rvert = \begin{cases}x,&x\ge0,\\-x,&x<0.\end{cases}\)
2. Корень из неотрицательного выражения: \(\sqrt{a}\) определён при \(a\ge0\).
3. Получаем кусочно-заданную функцию:
\( y = \begin{cases} \sqrt{-x}, & x<0,\\ \sqrt{x}, & x\ge0. \end{cases} \)
№479 учебника 2013-2022 (стр. 112):
\(a<0\) и \(b<0\), тогда
\(-a>0\) и \(-b>0\).
а) \(\sqrt{ab} =\sqrt{(-a)(-b)} =\sqrt{-a}\,\sqrt{-b}.\)
б) \(\sqrt{\frac{a}{b}}=\sqrt{\frac{-a}{-b}} =\frac{\sqrt{-a}}{\sqrt{-b}}.\)
Пояснения:
1) Область определения: подкоренное выражение должно быть неотрицательным.
При \(a<0,b<0\) имеем \(ab>0\) и \(\frac{a}{b}>0\),
тогда \(-a>0,-b>0\) имеем
\((-a)\cdot(-b)>0\) и \(\frac{-a}{-b}>0\).
2) Свойство корня из произведения:
\(\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}\) для \(a,b\ge0\).
3) Свойство корня из частного:
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) для \(a\ge0\) и \(b>0\).
Вернуться к содержанию учебника