Упражнение 1311 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 285
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1311 учебника 2023-2025 (стр. 285):
Постройте график функции, заданной формулой \(y = x + \dfrac{1}{x}\).
Подсказка
№1311 учебника 2023-2025 (стр. 285):
Вспомните:
- Что называют функцией, ее график.
- Координаты точки на координатной плоскости.
- Деление и дроби.
- Деление обыкновенных дробей.
- Деление рациональных чисел.
- Смешанные числа.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№1311 учебника 2023-2025 (стр. 285):
\(y = x + \dfrac{1}{x}\)
Область определения: \(x \ne 0\).
| \(x\) | \(-4\) | \(-3\) | \(-2\) | \(-1\) | \(-\frac12\) | \(-\frac14\) |
| \(y\) | \(-4\frac14\) | \(-3\frac13\) | \(-2\frac12\) | \(-2\) | \(-2\frac12\) | \(-4\frac14\) |
| \(x\) | \(\frac14\) | \(\frac12\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y\) | \(4\frac14\) | \(2\frac12\) | \(2\) | \(2\frac12\) | \(3\frac13\) | \(4\frac14\) |
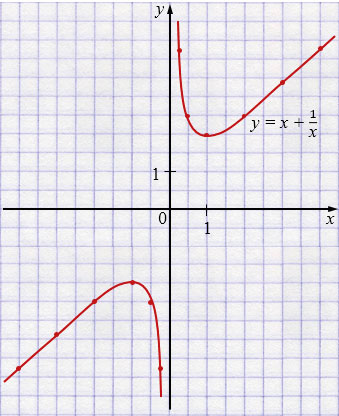
Пояснения:
Основные понятия:
Функция \(y = x + \dfrac{1}{x}\) — это сумма линейной функции \(y = x\) и обратной пропорциональности \(y = \dfrac{1}{x}\).
Область определения:
Так как знаменатель не может быть равен нулю, то функция определена при всех \(x \ne 0\).
Асимптоты:
Вертикальная асимптота — это прямая, где функция не определена, то есть \(x=0\).
Наклонная асимптота — прямая \(y=x\), так как при \(|x|\to\infty\) слагаемое \(\frac{1}{x}\) становится очень маленьким, и функция приближается к \(y=x\).
Форма графика:
Для \(x>0\) график проходит выше прямой \(y=x\), потому что \(\frac{1}{x}>0\), следовательно \(y>x\).
Для \(x<0\) график проходит ниже прямой \(y=x\), потому что \(\frac{1}{x}<0\), следовательно \(y
Таким образом, график состоит из двух ветвей: одна в первой четверти, другая — в третьей, обе приближаются к асимптотам \(x=0\) и \(y=x\), но не пересекают их.
Строим графики по точкам:
Если \(x = -4\), то
\(y = -4 + \dfrac{1}{-4} = -4 - \dfrac{1}{4} = -4\dfrac{1}{4}\).
Если \(x = -4\), то
\(y = -3 + \dfrac{1}{-3} = -3 - \dfrac{1}{3} = -3\dfrac{1}{3}\).
Если \(x = -2\), то
\(y = -2 + \dfrac{1}{-2} = -2 - \dfrac{1}{2} = -2\dfrac{1}{2}\).
Если \(x = -1\), то
\(y = -1 + \dfrac{1}{-1} = -1 - 1 = -2\).
Если \(x = -\frac12\), то
\(y = -\frac12 + \dfrac{1}{-\frac12} = -\frac12 - 2 = -2\dfrac{1}{2}\).
\(y = -\frac14 + \dfrac{1}{-\frac14} = -\frac14 - 4 = -4\dfrac{1}{4}\).
Аналогично находим значения функции для положительных значений \(x\).
Вернуться к содержанию учебника