Упражнение 906 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№906 учебника 2023-2025 (стр. 202):
(Для работы в парах.) Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами \(A\) и \(B\) и найдите пересечение и объединение этих множеств, если:
а) \(A\) — множество целых чисел, кратных 3, \(B\) — множество целых чисел, кратных 5;
б) \(A\) — множество целых чисел, кратных 3, \(B\) — множество целых чисел, кратных 15.
1) Распределите, кто выполняет задания для случая а), а кто - для случая б), и выполните их.
2) Проверьте друг у друга, верно ли выполнен рисунок и правильно ли найдены пересечение и объединение множеств \(A\) и \(B\).
3) Исправьте ошибки, если они допущены.
№906 учебника 2013-2022 (стр. 205):
Докажите, что если \(x>0\) и \(y>0\), то:
а) \(\dfrac{x}{y^{2}}+\dfrac{y}{x^{2}}\ge \dfrac{1}{x}+\dfrac{1}{y}\);
б) \(\dfrac{x^{2}}{y}+\dfrac{y^{2}}{x}\ge x+y.\)
Подсказка
№906 учебника 2023-2025 (стр. 202):
Вспомните:
- Что называют множеством.
- Объединение и пересечение множеств.
- Целые числа.
- Кратные числа.
№906 учебника 2013-2022 (стр. 205):
Вспомните:
- Доказательство неравенств.
- Разность квадратов двух выражений.
- Степень с натуральным показателем.
- Рациональные дроби.
- Сложение и вычитание рациональных дробей.
- Основное свойство рациональной дроби.
- Разложение многочленов на множители.
Ответ
№906 учебника 2023-2025 (стр. 202):
а) \(A\) — множество чисел, кратных 3.
\(B\) — множество чисел, кратных 5.
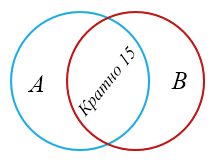
\(A \cap B\) — числа, кратные и 3, и 5.
\(A \cup B\) — числа, кратные 3 или 5.
б) \(A\) — множество чисел, кратных 3.
\(B \) — множество чисел, кратных 15.

\(A \cap B = B\),
\(A \cup B = A\).
Пояснения:
Пересечение множеств (\(\cap\)) — элементы, которые встречаются и в \(A\), и в \(B\). Объединение множеств (\(\cup\)) — все элементы, которые встречаются хотя бы в одном из множеств.
№906 учебника 2013-2022 (стр. 205):
а) \(\dfrac{x}{y^{2}}+\dfrac{y}{x^{2}}\ge \dfrac{1}{x}+\dfrac{1}{y}\), \(x>0\) и \(y>0\)
\( \left(\frac{x}{y^{2}} ^{\color{blue}{\backslash x}} -\frac{1}{x} ^{\color{blue}{\backslash y^2}}\right)+\left(\frac{y}{x^{2}} ^{\color{blue}{\backslash y}} -\frac{1}{y} ^{\color{blue}{\backslash x^2}} \right) =\)
\(=\frac{x^{2}-y^{2}}{xy^{2}}+\frac{y^{2}-x^{2}}{x^{2}y} =\)
\(=\frac{x^{2}-y^{2}}{xy^{2}}-\frac{x^{2}-y^{2}}{x^{2}y} =\)
\(=(x^2-y^2)\!\left(\frac{1}{xy^{2}} ^{\color{blue}{\backslash x}}-\frac{1}{x^{2}y} ^{\color{blue}{\backslash y}}\right) =\)
\(=(x-y)(x+y)\cdot\frac{x-y}{x^2y^{2}} =\)
\(=\frac{(x-y)^{2}(x+y)}{x^{2}y^{2}}\ge 0 \) для любых \(x>0\) и \(y>0\)
Что и требовалось доказать.
б) \(\dfrac{x^{2}}{y}+\dfrac{y^{2}}{x}\ge x+y\), \(x>0\) и \(y>0\)
\(\dfrac{x^{2}}{y}+\dfrac{y^{2}}{x} - (x+y)=\)
\(=\dfrac{x^{2}}{y}^{\color{blue}{\backslash x}}+\dfrac{y^{2}}{x}^{\color{blue}{\backslash y}} - x^{\color{blue}{\backslash xy}}-y^{\color{blue}{\backslash xy}}=\)
\(=\dfrac{x^{3}+ y^3 -x^2y -xy^2}{xy} =\)
\(=\dfrac{(x^{3} -x^2y) -(xy^2 - y^3)}{xy} =\)
\(=\dfrac{x^2(x - y) - y^2(x - y)}{xy} =\)
\(=\dfrac{(x - y)(x^2 - y^2)}{xy} =\)
\(=\dfrac{(x - y)(x - y)(x+y)}{xy} =\)
\(=\dfrac{(x - y)^2(x+y)}{xy} \ge 0\) для любых \(x>0\) и \(y>0\)
Что и требовалось доказать.
Пояснения:
При доказательстве составляем разность левой и правой частей неравенства и показываем, что эта разность сохраняет знак при любых указанных значениях переменных.
Составив разности приводим дроби к общему знаменателю и выполняем преобразования. При этом помним:
- разности квадратов:
\(x^2 - y^2 = (x - y)(x + y)\);
- квадрат любого числа всегда принимает неотрицательные значения;
- произведение положительных чисел является положительным числом.
Вернуться к содержанию учебника