Подмножество. Операции над множествами. Объединение и пересечение множеств
Рассмотрим множества {2, 4, 6, 8} и {4; 8}. Каждый элемент второго множества принадлежит также и первому, но не каждый элемент первого множества принадлежит второму множеству. Тогда говорят, что второе множество является подмножеством первого.
| Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В. Пустое множество считают подмножеством любого другого множества. |
Если множество А является подмножеством множества В, то в символическом виде это записывают: 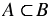 или
или 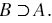 (читают: "множество А - подмножество множества В" или "множество В содержит множество А").
(читают: "множество А - подмножество множества В" или "множество В содержит множество А").
Для иллюстрации соотношений между множествами пользуются схемами, которые называют диаграммами Эйлера. Изобразить то, что 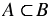 можно следующим образом:
можно следующим образом:
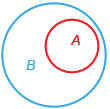
Если использовать данный рисунок можно сделать такие выводы:
1) для того чтобы элемент 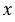 принадлежал множеству В, достаточно, чтобы он принадлежал множеству А;
принадлежал множеству В, достаточно, чтобы он принадлежал множеству А;
2) для того чтобы элемент 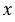 принадлежал множеству А, необходимо, чтобы он принадлежал множеству В.
принадлежал множеству А, необходимо, чтобы он принадлежал множеству В.
Определение:
| Множество, состоящее из элементов, входящих в каждое из данных множеств, называется их пересечением. То есть пересечением множеств А и В называют множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В. |
Рассмотрим множество А = {1, 3, 5, 7, 9} и В = {1, 3, 9}. Пересечение множеств А и В составляют элементы 1 и 9.
Пересечение множеств обозначают с помощью символа - 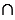 . Тогда для множеств А и В можем записать:
. Тогда для множеств А и В можем записать:
А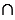 В = {1, 9}.
В = {1, 9}.
Изобразить пересечение множеств А и В с помощью диаграмм Эйлера можно следующим образом:
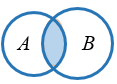
Определение:
Областью определения уравнения 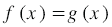 называют множество значений переменной называют множество значений переменной 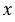 , при которых имеют смысл обе части уравнения. , при которых имеют смысл обе части уравнения. |
Определение:
| Множество, состоящее из элементов, входящих хотя бы в одно из данных множеств, называется их объединением. То есть объединением множеств А и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств: или множеству А, или множеству В. |
Рассмотрим два множества А = {1, 7, 9, 11} и В = {1, 3, 9, 13}. Объединение множеств А и В составляют элементы 1, 3, 7, 9, 11 и 13.
Объединение множеств обозначают с помощью символа - 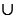 . Тогда для множеств А и В можем записать:
. Тогда для множеств А и В можем записать:
А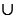 В = {1, 3, 7, 9, 11, 13}.
В = {1, 3, 7, 9, 11, 13}.
Изобразить объединение множеств А и В с помощью диаграмм Эйлера можно следующим образом:
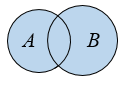
Если у двух множеств нет общих элементов, то пересечением этих множеств является пустое множество. Например, если Х = {1, 3, 5, 7, 9} и У = {0, 2, 4, 6, 8}, то Х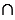 У =
У = 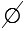 , а Х
, а Х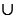 У = {0, 1, 2. 3, 4, 5, 6, 7, 8, 9}.
У = {0, 1, 2. 3, 4, 5, 6, 7, 8, 9}.
Советуем посмотреть:
Правило встречается в следующих упражнениях:
5 класс
Задание 896, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 897, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 898, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 909, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 910, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 10, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Задание 1.138, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.141, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.143, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.160, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.162, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.163, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.44, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.188, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.91, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.131, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Упражнение 2, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 443, Мерзляк, Полонский, Якир, Учебник
Номер 445, Мерзляк, Полонский, Якир, Учебник
Номер 450, Мерзляк, Полонский, Якир, Учебник
Номер 452, Мерзляк, Полонский, Якир, Учебник
Номер 457, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Упражнение 902, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 903, Макарычев, Миндюк, Нешков, Суворова, Учебник