Упражнение 528 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№528 учебника 2023-2025 (стр. 120):
Телевизор имеет плоский экран прямоугольной формы. В паспорте к телевизору указано, что длина экрана относится к ширине как 4 : 3, а диагональ равна 25 дюймам. Найдите длину и ширину экрана в дюймах; в сантиметрах (1 дюйм = 2,54 см).
№528 учебника 2013-2022 (стр. 121):
Путь свободно падающего тела вычисляется по формуле
\(s = \frac{g\,t^2}{2},\) где \(t\) (с) — время, \(g\approx10\) м/с², \(s\) (м) — пройденный путь. Через сколько секунд от начала падения камень достигнет дна шахты глубиной 80 м?
Подсказка
№528 учебника 2023-2025 (стр. 120):
Вспомните:
- Что называют отношением двух чисел.
- Теорему Пифагора.
- Решение неполных квадратных уравнений.
- Свойства уравнений.
- Деление и дроби.
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем
- Подобные слагаемые.
- Умножение десятичных дробей.
№528 учебника 2013-2022 (стр. 121):
Вспомните:
- Решение неполных квадратных уравнений.
- Свойства уравнений.
- Деление и дроби.
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
Ответ
№528 учебника 2023-2025 (стр. 120):
Длина экрана относится к ширине как
4 : 3.
Пусть длина экрана равна \(4x\) (дюймов), тогда ширина равна \(3x\) (дюймов). Диагональ телевизора равна 25 дюймов.
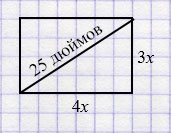
По теореме Пифагора составим уравнение::
\( (3x)^2 + (4x)^2 = 25^2\)
\(9x^2 + 16x^2 = 625 \)
\(25x^2 = 625 \)
\(x^2 = 25\)
\(x_1 = -\sqrt{25}\)
\(x_1 = -5\) - не удовлетворяет условию.
\(x_2 = \sqrt{25}\)
\(x_2 = 5\)
1 дюйм = 2,54 см
1) \(3\cdot5 = 15\) (дюймов) =
\(=15\cdot2,54 = 38,1\) (см) - ширина экрана.
| × | 2 | 5 | 4 | |
| 1 | 5 | |||
| + | 1 | 2 | 7 | 0 |
| 2 | 5 | 4 | ||
| 3 | 8 | 1 | 0 |
2) \(4\cdot5 = 20\) (дюймов) =
\(=20\cdot2,54 =50,8 \) (см) - длина экрана.
Ответ: 15 дюймов = 38,1 см;
20 дюймов = 50,8 см.
Пояснения:
1. Стороны экрана телевизора, обозначенные \(3x\) и \(4x\), образуют прямой угол. Диагональ экрана — гипотенуза.
2. По теореме Пифагора составляем уравнение \( (\,3x)^2 + (\,4x)^2 = 25^2 \).
3. При преобразовании уравнения использовали свойство степени:
\((ab)^n = a^nb^n\).
4. После преобразования получили уравнение \(x^2 = 25\). Откуда извлечением корня нашли \(x\). Взяли только положительное значение, так как длина не может быть отрицательной.
5. Получили \(x=5\), затем нашли размеры в дюймах:
\(3x=15\) и \(4x=20\)
и перевели их в сантиметры, умножив на 2,54.
№528 учебника 2013-2022 (стр. 121):
\(s = \frac{g\,t^2}{2},\)
\(g\approx10\) м/с², \(s = 80\) м.
\( 80 = \frac{10\,t^2}{2}\)
\(80 = 5t^2 \)
\(t^2 = \frac{80}{5}\)
\(t^2= 16 \)
\(t_1 = -\sqrt{16} \)
\(t_1 = -4 \) - не удовлетворяет условию.
\(t_2 = \sqrt{16}\)
\(t_1 = 4 \)
Ответ: через 4 с.
Пояснения:
– Формула пути при свободном падении: \(s=\frac{gt^2}{2}\).
– Подставили \(g=10\) и \(s=80\) в формулу, получили квадратное уравнение \(5t^2=80\).
– Решили его через извлечение корня: \(x=\sqrt{16}=4\) (выбрали положительный корень, так как время положительно).
Вернуться к содержанию учебника