Упражнение 614 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№614 учебника 2023-2025 (стр. 134):
Вычислите значение выражения
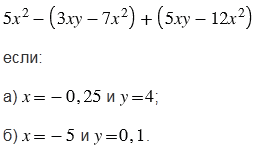
№614 учебника 2013-2022 (стр. 136):
Выполните умножение:
а) \(2x(x^2 - 7x - 3)\);
б) \(-4b^2(5b^2 - 3b - 2)\);
в) \((3a^3 - a^2 + a)(-5a^3)\);
г) \((y^2 - 2{,}4y + 6)\cdot1{,}5y\);
д) \(-0{,}5x^2(-2x^2 - 3x + 4)\);
е) \((-3y^2 + 0{,}6y)(-1{,}5y^3)\).
Подсказка
№614 учебника 2023-2025 (стр. 134):
Вспомните:
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение десятичных дробей.
- Умножение рациональных чисел.
№614 учебника 2013-2022 (стр. 136):
Вспомните:
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Умножение рациональных чисел.
- Умножение десятичных дробей.
- Свойства степени с натуральным показателем.
Ответ
№614 учебника 2023-2025 (стр. 134):
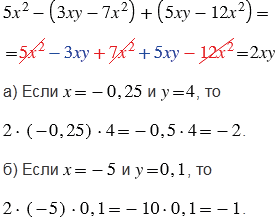
Пояснения:
Сначала нужно упростить выражение. Чтобы упростить выражение, нужно раскрыть скобки и привести подобные слагаемые (в решении выделены одинаковым цветом). Подобные слагаемые, которые в сумме дают ноль, вычеркнуты.
При раскрытии скобок помним:
1) если перед скобками стоит знак "+", то можно опустить скобки и этот знак "+", сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком "+";
2) Если перед скобками стоит знак " - ", то можно опустить скобки и этот знак "-", изменив знаки слагаемых, стоящих в скобках на противоположные. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком " - ".
Затем в полученное упрощенное выражение вместо переменных нужно подставить числа и выполнить вычисления.
№614 учебника 2013-2022 (стр. 136):
а) \( 2x(x^2 - 7x - 3) =\)
\(=2x^3 - 14x^2 - 6x. \)
б) \( -4b^2(5b^2 - 3b - 2) =\)
\( = -20b^4 + 12b^3 + 8b^2. \)
в) \( (3a^3 - a^2 + a)(-5a^3) = \)
\( = -15a^6 + 5a^5 - 5a^4. \)
г) \( (y^2 - 2{,}4y + 6)\cdot1{,}5y = \)
\( = 1{,}5y^3 - 3{,}6y^2 + 9y. \)
д) \( -0{,}5x^2(-2x^2 - 3x + 4) = \)
\( = x^4 + 1{,}5x^3 - 2x^2. \)
е) \( (-3y^2 + 0{,}6y)(-1{,}5y^3) = \)
\( = 4{,}5y^5 - 0{,}9y^4. \)
Пояснения:
Для каждого случая применён распределительный закон: множитель вне скобок умножается на каждый член внутри скобок.
\( X(Y+Z)=XY+XZ \).
Выполнены поочерёдно: возведение в степень, умножение коэффициентов и переменных с учётом показателей, затем приведены полученные одночлены.
Вернуться к содержанию учебника