стр. 27-28. Проверьте себя - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Проверьте себя
Вопрос
Проверочная работа
1. Сравните числа:
а) -8 и 0;
б) 0,001 и 0;
в) -0,01 и 0;
г) 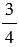 и 0.
и 0.
2. Сравните числа:
а) 3,4 и -3,47;
б) 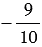 и
и 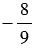 ;
;
в) 0,317 и 0,0317;
г) 20,14 и -20,14;
д) 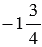 и .
и .
3. Расположите числа 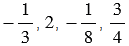 в порядке возрастания.
в порядке возрастания.
4. Какие целые числа можно поставить вместо 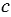 , чтобы получилось верное двойное неравенство:
, чтобы получилось верное двойное неравенство:
а) -6 < 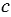 < 1;
< 1;
б) -93 < 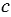 < -83;
< -83;
в) -1 < 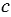 < 1?
< 1?
Подсказка
Вспомните:
- Положительные и отрицательные числа, целые числа.
- Сравнение положительных и отрицательных чисел.
- Модуль числа.
- Сравнение обыкновенных дробей.
- Приведение дробей к общему знаменателю.
- Основное свойство дроби.
- Сравнение десятичных дробей.
- Десятичная запись дробных чисел.
Ответ
Проверочная работа
1. а) -8 < 0;
б) 0,001 > 0;
в) -0,01 < 0;
г) 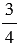 > 0.
> 0.
2. а) 3,4 > -3,47;
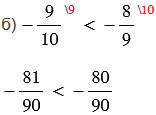
в) 0,317 > 0,0317;
г) 20,14 > -20,14;
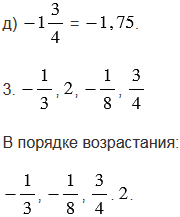
4. 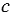 - целое число.
- целое число.
а) -6 < 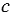 < 1
< 1
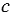 = -5, -4, - 3, -2, -1, 0.
= -5, -4, - 3, -2, -1, 0.
б) -93 < 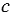 < -83
< -83
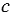 = -92, -91, -90, - 89, -88, -87, -86, -85, -84.
= -92, -91, -90, - 89, -88, -87, -86, -85, -84.
в) -1 < 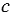 < 1
< 1
= 0.
Пояснения:
При сравнении помним следующие правила:
1) любое положительное число больше любого отрицательного числа;
2) из двух отрицательных чисел меньше то, модуль которого больше (модуль всегда принимает неотрицательные значения);
3) любое отрицательное число меньше нуля, любое положительное число больше нуля.
4) чтобы сравнить две положительные десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно, то есть из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей;
5) из двух положительных дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше (если у дробей разные числители и знаменатели, то их сначала нужно привести к общему знаменателю, используя основное свойство дроби, а затем выполнить сравнение);
6) из двух положительных дробей с одинаковыми числителями больше та, у которой знаменатель меньше, а меньше та, у которой знаменатель больше.
Вернуться к содержанию учебника