Задание 2.283 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.283 учебника 2023-2024 (стр. 83):
Из двух городов одновременно навстречу друг другу вышли два поезда и встретились через 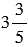 ч. Найдите расстояние между городами, если скорость одного поезда равна 75 км/ч, а скорость другого составляет
ч. Найдите расстояние между городами, если скорость одного поезда равна 75 км/ч, а скорость другого составляет 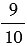 от скорости первого поезда.
от скорости первого поезда.
№2.283 учебника 2021-2022 (стр. 77):
Выполните действия:
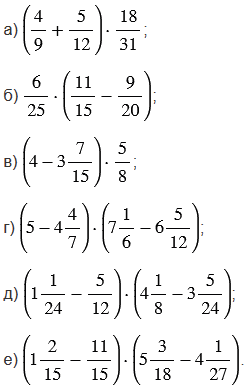
Подсказка
№2.283 учебника 2023-2024 (стр. 83):
Вспомните:
- Задачи на движение.
- Десятичные дроби.
- Умножение десятичных дробей.
- Сложение десятичных дробей.
- Основное свойство дроби.
№2.283 учебника 2021-2022 (стр. 77):
Вспомните:
- Порядок выполнения действий.
- Умножение обыкновенных дробей.
- Сложение и вычитание смешанных чисел.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Наименьшее общее кратное.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Основное свойство дроби (сокращение дробей).
- Неправильные дроби.
Ответ
№2.283 учебника 2023-2024 (стр. 83):
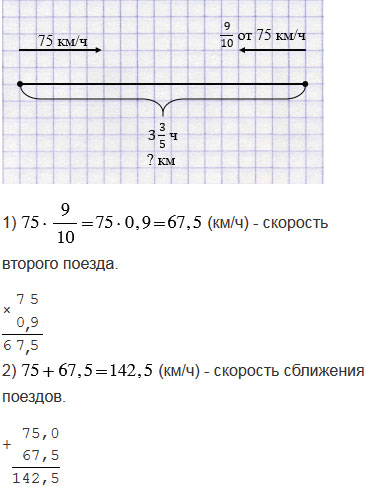


№2.283 учебника 2021-2022 (стр. 77):
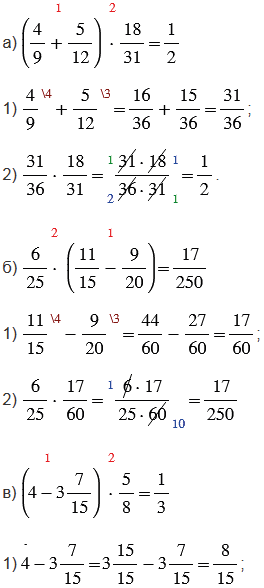
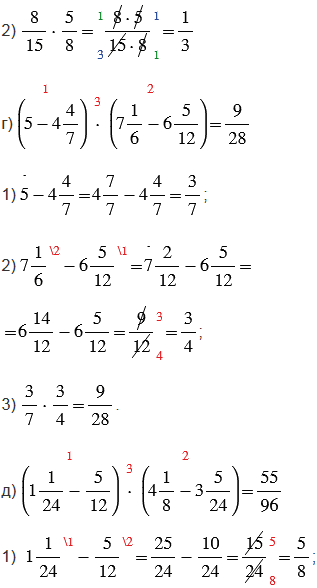
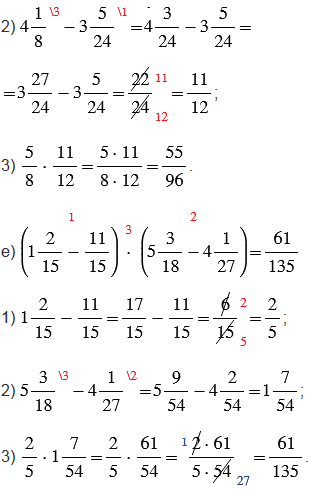
Пояснения:
Действиями первой ступени называют сложение и вычитание чисел, а действиями второй ступени - умножение и деление чисел.
При вычислении значений выражений порядок выполнения действий определяют следующие правила:
1. Если выражение содержит только действия одной ступени и в нем нет скобок, то действия выполняют по порядку слева направо.
2. Если в выражении нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени.
3. Если в выражении есть скобки есть скобки, то сначала выполняют действия в скобках (учитывая правила 1 и 2).
Красные числа, стоящие сверху над действиями, показывают в каком порядке нужно выполнять действия.
Вычисления выполняем по следующим правилам:
1) чтобы найти сумму смешанных чисел, надо: дробные части этих чисел привести к наименьшему общему знаменателю; отдельно выполнить сложение целых и отдельно дробных частей; при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель), выделить целую часть (когда числитель больше знаменателя) и прибавить ее к полученной целой части;
2) чтобы найти разность натурального числа и дроби или натурального числа и смешанного числа, надо: натуральное число уменьшить на единицу и единицу представить в виде неправильной с равными числителем и знаменателем, которые должны быть равны знаменателю дробной части вычитаемого; отдельно вычесть целые и отдельно дробные части и результаты сложить.
3) чтобы найти разность смешанных чисел, надо: дробные части этих чисел привести к наименьшему общему знаменателю; если дробная часть уменьшаемого больше дробной части вычитаемого, то надо отдельно вычесть целые и отдельно дробные части и результаты сложить; если дробная часть уменьшаемого меньше дробной части вычитаемого, то надо превратить ее в неправильную дробь, уменьшив на единицу целую часть, и отдельно вычесть целые и отдельно дробные части и результаты сложить; при необходимости сократить дробь (разделить числитель и знаменатель дроби на их наибольший общий делитель);
4) чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним;
5) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей;
6) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Вернуться к содержанию учебника