Задание 2.285 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.285 учебника 2023-2024 (стр. 83):
Двое друзей вышли навстречу друг другу и встретились в условном месте. Какое расстояние было изначально между ними, если первый шел  ч со скоростью
ч со скоростью  км/ч, а второй -
км/ч, а второй -  ч со скоростью
ч со скоростью 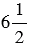 км/ч?
км/ч?
№2.285 учебника 2021-2022 (стр. 78):
Выполните действие:
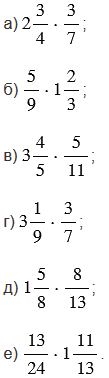
Подсказка
№2.285 учебника 2023-2024 (стр. 83):
Вспомните:
- Смешанные числа.
- Неправильные дроби.
- Умножение смешанных чисел.
- Основное свойство дроби.
- Деление и дроби.
- Деление с остатком.
- Сложение смешанных чисел.
- Сложение дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Наименьшее общее кратное.
- Сложение дробей с одинаковыми знаменателями.
- Разложение на простые множители.
№2.285 учебника 2021-2022 (стр. 78):
Вспомните:
- Смешанные числа.
- Неправильные дроби.
- Умножение смешанных чисел и обыкновенных дробей.
- Сокращение дробей.
- Деление и дроби.
- Деление с остатком.
Ответ
№2.285 учебника 2023-2024 (стр. 83):



Правила, по которым выполняем вычисления:
1) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей (чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа), а затем воспользоваться правилом умножения дробей, если в результате умножения дробь получается неправильной, нужно выделить целую часть. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
2) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей;
3) чтобы найти сумму смешанных чисел, надо: дробные части этих чисел привести к наименьшему общему знаменателю; отдельно выполнить сложение целых и отдельно дробных частей;
4) чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Если сложно найти наименьший общий знаменатель при сложении дробей, можно использовать разложение на простые множители:
16 = 2222,
30 = 235.
НОК(16; 30) = 222235 = 240 - наименьший общий знаменатель дробей, знаменатели которых 16 и 30.
№2.285 учебника 2021-2022 (стр. 78):
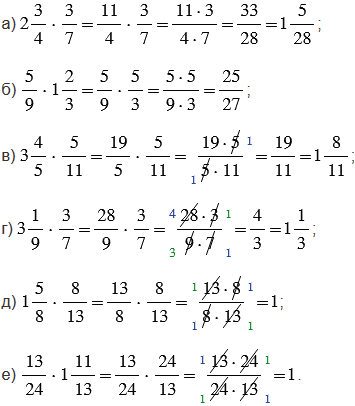
Пояснения:
Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей, согласно которому произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения.
Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Если при вычислениях получилась неправильная дробь, преобразуем ее в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
Вернуться к содержанию учебника