Задание 2.33 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.33 учебника 2023-2024 (стр. 47):
Вычислите значение выражения:

№2.33 учебника 2021-2022 (стр. 41):
Напишите двузначные числа меньше 200, разложение которых на простые множители состоит из двух или трех одинаковых множителей. Как называют эти числа?
Подсказка
№2.33 учебника 2023-2024 (стр. 47):
Вспомните:
- Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями.
- Сложение и вычитание смешанных чисел.
- Сокращение дробей.
- Умножение обыкновенных дробей.
- Деление обыкновенных дробей.
№2.33 учебника 2021-2022 (стр. 41):
Вспомните:
- Разложение на простые множители.
- Какие числа называют простыми.
- Квадрат и куб числа.
- Сравнение чисел.
Ответ
№2.33 учебника 2023-2024 (стр. 47):

Пояснения:
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Чтобы найти сумму (разность) двух смешанных чисел, надо отдельно сложить (вычесть) их целые и дробные части.
Если при вычислениях получается сократимая дробь, то сокращаем ее (числитель и знаменатель делим на их общий делитель).
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 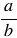 является число
является число 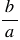 .
.
При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения.
№2.33 учебника 2021-2022 (стр. 41):
25 = 5 • 5 = 52;
49 = 7 • 7 = 72;
27 = 3 • 3 • 3 = 33.
Ответ: эти числа называют квадрат числа и куб числа.
Пояснения:
Представление числа в виде произведения его простых делителей называют разложением числа на простые множители.
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число.
Скорее всего в учебнике допущена опечатка и нужно написать еще и трехзначные числа меньше 200, разложение которых на простые множители состоит из двух или трех одинаковых множителей.
121 = 11 • 11 = 112;
169 = 13 • 13 = 132;
125 = 5 • 5 • 5 = 53.
Вернуться к содержанию учебника