Задание 489 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№489 учебника 2013-2022 (стр. 132):
Докажите, что площадь равностороннего треугольника вычисляется по формуле 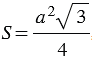 , где
, где 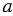 - сторона треугольника. Найдите площадь равностороннего треугольника, если его сторона равна:
- сторона треугольника. Найдите площадь равностороннего треугольника, если его сторона равна:
а) 5 см; б) 1,2 см; в) 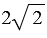 дм.
дм.
№489 учебника 2023-2024 (стр. 129):
Подсказка
№489 учебника 2013-2022 (стр. 132):
Вспомните:
- Какой треугольник называется равносторонним.
- Свойства равностороннего треугольника.
- Как найти площадь треугольника.
- Теорему Пифагора.
- Что такое высота треугольника.
№489 учебника 2023-2024 (стр. 129):
Вспомните:
- Что называют трапецией.
- Какая точка является серединой отрезка.
- Какие прямые называют параллельными.
- Терема Фалеса.
Ответ
№489 учебника 2013-2022 (стр. 132):
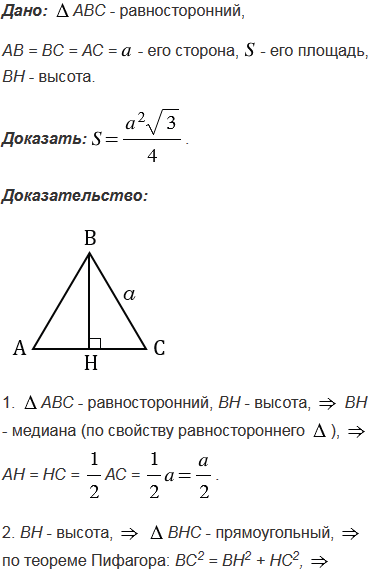



№489 учебника 2023-2024 (стр. 129):
Дано: АВСD - трапеция.
Доказать: средняя линия трапеции параллельна основаниям трапеции и равна их полусумме
Доказательство:
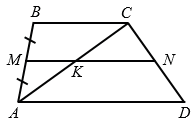
Пусть М - середина АВ, проведем через М прямую МN, параллельную АD и ВС, т.е. МN 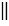 ВС и МN
ВС и МN 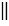 АD,
АD,  по теореме Фалеса точки К и N середины отрезков АС и СD,
по теореме Фалеса точки К и N середины отрезков АС и СD,  МN - средняя линия трапеции АВСD.
МN - средняя линия трапеции АВСD.
МК - средняя линия 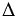 АВС,
АВС, 
МК = 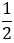 ВС.
ВС.
КN - средняя линия 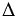 АСD,
АСD, 
КN = 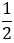 АD.
АD.
МN = МК + КN = 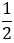 ВС +
ВС + 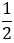 АD =
АD =
= 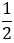 (ВС + АD).
(ВС + АD).
Что и требовалось доказать.
Пояснения:
Пусть точка М - середина АВ, проведем через М прямую МN, параллельную основаниям трапеции ВС и АD, т.е.
МN 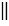 ВС и МN
ВС и МN 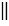 АD.
АD.
Согласно теореме Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую,то они отсекут на второй прямой равные между собой отрезки. Значит, точки К и N середины отрезков АС и СD, следовательно, МN - средняя линия трапеции АВСD, а МК и КN - средние линии треугольников АВС и АСD соответственно.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Тогда из того, что МК - средняя линия 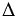 АВС, получаем МК =
АВС, получаем МК = 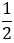 ВС, а из того, что КN - средняя линия
ВС, а из того, что КN - средняя линия 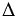 АСD, получаем КN =
АСD, получаем КN = 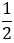 АD.
АD.
Точка К делит отрезок МN на два отрезка МК и КN, тогда:
МN = МК + КN = 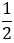 ВС +
ВС + 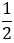 АD =
АD =
= 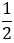 (ВС + АD).
(ВС + АD).
Вернуться к содержанию учебника