Задание 392 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№392 учебника 2013-2022 (стр. 106):
Основания прямоугольной трапеции равны 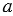 и
и 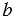 , один из углов равен
, один из углов равен 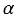 . Найдите: а) большую боковую сторону трапеции, если
. Найдите: а) большую боковую сторону трапеции, если 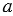 = 4 см,
= 4 см, 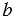 = 7 см,
= 7 см, 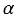 = 600; б) меньшую боковую сторону трапеции, если
= 600; б) меньшую боковую сторону трапеции, если 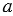 = 10 см,
= 10 см, 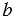 = 15 см,
= 15 см, 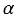 = 450.
= 450.
№392 учебника 2023-2024 (стр. 112):
Подсказка
№392 учебника 2013-2022 (стр. 106):
Вспомните:
- Какая трапеция называется прямоугольной.
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
- Какой треугольник называется равнобедренным.
- Признаки равнобедренного треугольника.
- Теорему о сумме углов треугольника.
- Какая фигура называется параллелограммом.
- Признаки параллелограмма.
№392 учебника 2023-2024 (стр. 112):
Вспомните:
- Что такое ось симметрии, симметричные фигуры.
- Что такое треугольник.
- Длина отрезка.
Ответ
№392 учебника 2013-2022 (стр. 106):
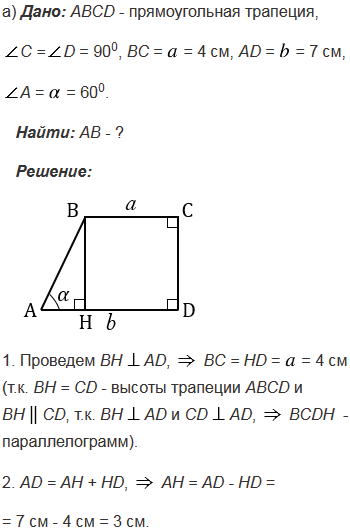






№392 учебника 2023-2024 (стр. 112):
Дано: ВО - ось симметрии 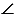 АВС,
АВС, 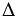 ВА1С1 симметричен
ВА1С1 симметричен 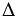 АВС относительно прямой ВО, ВА = 5,4 см = 54 мм, ВС = 35 мм.
АВС относительно прямой ВО, ВА = 5,4 см = 54 мм, ВС = 35 мм.
Найти: А1С и АС1.
Решение:
1. Точка В симметрична сама себе, точки С и С1 симметричны относительно прямой р, 
ВС1 = ВС = 35 мм.
2. ВС1 + АС1 = ВА,  АС1 = ВА - ВС1 = 54 мм - 35 мм = 19 мм.
АС1 = ВА - ВС1 = 54 мм - 35 мм = 19 мм.
3. Точка В симметрична сама себе, точки А и А1 симметричны относительно прямой р, 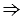
ВА1 = ВА = 54 мм.
4. ВС + А1С = ВА1, 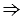 А1С = ВА1 - ВС = 54 мм - 35 мм = 19 мм.
А1С = ВА1 - ВС = 54 мм - 35 мм = 19 мм.
Ответ: А1С = АС1 = 19 мм.
Пояснения:
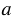 , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно.
Две точки А и А1 называются симметричными относительно прямой р, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1.
Прямая ВО — ось симметрии угла АВС. Треугольник ВА1С1 симметричен треугольнику АВС относительно прямой ВО, значит, точка В симметрична сама себе, точки С и С1 симметричны относительно прямой р, поэтому ВС1 = ВС = 35 мм.
Точка С1 лежит между точками В и А, значит, ВС1 + АС1 = ВА, откуда
АС1 = ВА - ВС1 = 54 мм - 35 мм = 19 мм.
Также точка В симметрична сама себе, точки А и А1 симметричны относительно прямой р, следовательно, ВА1 = ВА = 54 мм.
Точка С1 лежит между точками В и А1, значит, ВС + А1С = ВА1, откуда
А1С = ВА1 - ВС = 54 мм - 35 мм = 19мм.
Вернуться к содержанию учебника