Задание 389 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№389 учебника 2013-2022 (стр. 105):
Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны.
№389 учебника 2023-2024 (стр. 111):
Подсказка
№389 учебника 2013-2022 (стр. 105):
Вспомните:
- Какая трапеция называется равнобедренной.
- Что такое диагональ многоугольника.
- Какая фигура называется параллелограммом, его свойства.
- Теорему о соответственных углах.
- Какой треугольник называется равнобедренным.
- Признаки равнобедренного треугольника.
№389 учебника 2023-2024 (стр. 111):
Вспомните:
- Какие точки называют симметричными относительно прямой.
- Что такое длина отрезка.
Ответ
№389 учебника 2013-2022 (стр. 105):

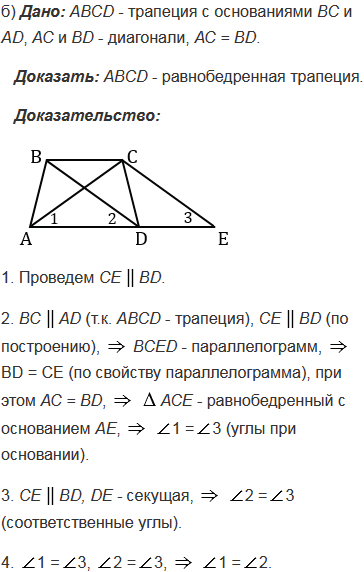





№389 учебника 2023-2024 (стр. 111):
а) Дано: точки А1, В1, С1 симметричны точкам А, В, С относительно некоторой прямой, АВ = 2 дм, АС = 10 дм, ВС = 80 см.
Найти: лежат ли точки А1, В1, С1 на одной прямой?
Решение:
80 см = 8 дм
2 дм + 8 дм = 10 дм, 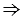 АВ + ВС = АС,
АВ + ВС = АС, 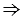 точки А, В, С лежат на одной прямой,
точки А, В, С лежат на одной прямой, 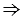 точки А1, В1, С1 лежат на одной прямой.
точки А1, В1, С1 лежат на одной прямой.
Ответ: да, лежат.
б) Дано: точки А1, В1, С1 симметричны точкам А, В, С относительно некоторой прямой, АВ = 1,1 см, В1С1 = 5 см, СА = 6 см.
Найти: лежат ли точки А1, В1, С1 на одной прямой?
Решение:
Точки А1, В1, С1 симметричны точкам А, В, С относительно некоторой прямой, 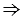 ВС = В1С1 = 5 см
ВС = В1С1 = 5 см
1,1 см + 5 см = 6,1 см 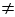 6 см,
6 см, 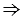 АВ + ВС
АВ + ВС 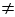 АС,
АС, 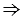 точки А, В, С не лежат на одной прямой,
точки А, В, С не лежат на одной прямой, 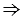 точки А1, В1, С1 не лежат на одной прямой.
точки А1, В1, С1 не лежат на одной прямой.
Ответ: нет, не лежат.
Пояснения:
Две точки А и А1 называются симметричными относительно прямой р, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Расстояния между данными точками и симметричными им точками сохранятся.
Если три точки лежат на одной прямой, то в таком случае сумма длин двух меньших отрезков, должна быть равна длине большего отрезка. Так, для трех точек А, В и С, лежащих на одной прямой, в том случае, когда точка В лежит между точками А и С, должно выполняться равенство: АВ + ВС = АС.
Вернуться к содержанию учебника