Задание 353 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№353 учебника 2013-2022 (стр. 96):
Постройте точку, лежащую на данной окружности и равноудаленную от концов данного отрезка. Сколько решений может иметь задача?
№353 учебника 2023-2024 (стр. 104):
Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными из точки А. Найдите угол ВАС, если середина отрезка АО лежит на окружности.
Подсказка
№353 учебника 2013-2022 (стр. 96):
Вспомните:
- Что такое окружность.
- Что такое отрезок.
- Как построить середину отрезка.
№353 учебника 2023-2024 (стр. 104):
Вспомните:
- Что такое окружность, ее элементы.
- Что называется касательной к окружности, ее свойства.
- Что такое угол.
- Какая точка называется серединой отрезка.
- Какой треугольник называется прямоугольным.
- Свойства прямоугольных треугольников.
Ответ
№353 учебника 2013-2022 (стр. 96):
Дано: окружность(О), отрезок АВ.
Построить: точку М на окружности так, что АМ = ВМ.
Построение:
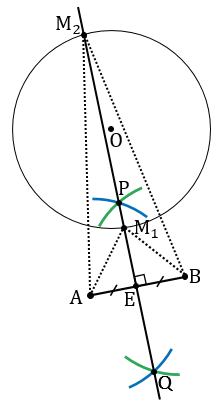
Доказательство:
В 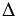 АВМ1: ЕМ1 - медиана и высота по построению,
АВМ1: ЕМ1 - медиана и высота по построению, 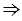
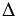 АВМ1 - равнобедренный (свойство равнобедренного треугольника),
АВМ1 - равнобедренный (свойство равнобедренного треугольника),  АМ1 = ВМ1. Аналогично доказывается, что АМ2 = ВМ2,
АМ1 = ВМ1. Аналогично доказывается, что АМ2 = ВМ2,  2 решения.
2 решения.
Ответ: задача может иметь 2 решения, 1 решение или не иметь решений.
Пояснения:
Строим с помощью циркуля окружность произвольного радиуса с центром в точке О и с помощью линейки отрезок АВ.
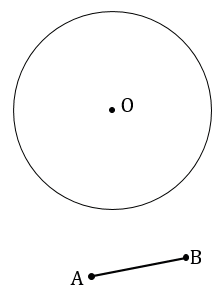
Далее находим середину отрезка АВ, т.е. строим серединный перпендикуляр. Для этого с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом).
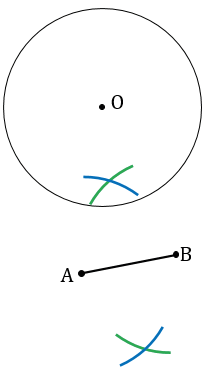
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q, проведем через эти точки с помощью линейки прямую РQ, которая пересечет отрезок АВ в точке Е и окружность с центром в точке О в точках М1 и М2. РQ - серединный перпендикуляр для отрезка АВ, точка Е - середина отрезка АВ.
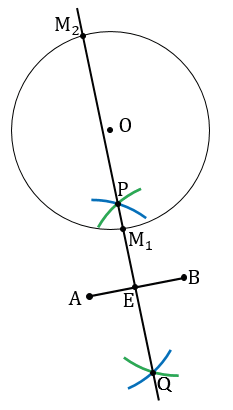
Докажем, что точки М1 и М2 - искомые точки, для которых выполняются условия АМ1 = ВМ1 и АМ2 = ВМ2.

Рассмотрим 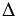 АВМ1: ЕМ1 - медиана, т.к. точка Е - середина АВ по построению, и ЕМ1 - высота, т.к. РQ - перпендикуляр по построению, тогда, учитывая то, что если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника, получим, что
АВМ1: ЕМ1 - медиана, т.к. точка Е - середина АВ по построению, и ЕМ1 - высота, т.к. РQ - перпендикуляр по построению, тогда, учитывая то, что если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника, получим, что 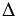 АВМ1 равнобедренный с основанием АВ, следовательно, АМ1 = ВМ1 (боковые стороны равнобедренного треугольника). Аналогично доказывается равенство АМ2 = ВМ2.
АВМ1 равнобедренный с основанием АВ, следовательно, АМ1 = ВМ1 (боковые стороны равнобедренного треугольника). Аналогично доказывается равенство АМ2 = ВМ2.
В данных условиях получили, что на данной окружности можно построить две точки М1 и М2, для которых выполняются условия АМ1 = ВМ1 и АМ2 = ВМ2, т.е. задача будет иметь два решения.
Если перпендикуляр РQ будет касаться окружности, то решение будет одно, если РQ не будет пересекать окружность, то решений не будет.
№353 учебника 2023-2024 (стр. 104):
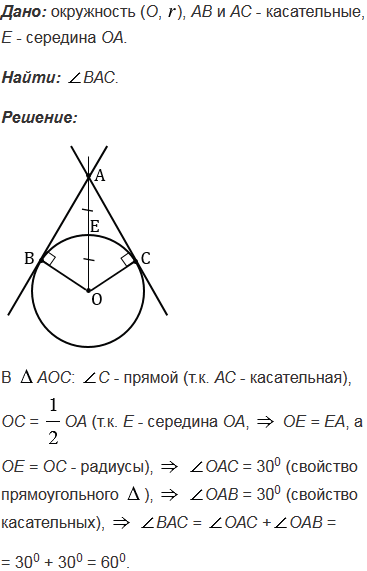


Вернуться к содержанию учебника