Задание 354 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№354 учебника 2013-2022 (стр. 96):
Через три данные точки проведите окружность. Всегда ли задача имеет решение?
№354 учебника 2023-2024 (стр. 104):
На рисунке 162 ОВ = 3 см, ОА = 6 см. Найдите 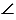 3 и
3 и 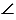 4.
4.
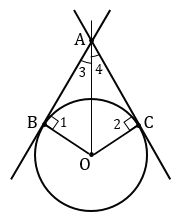
Рис. 162
Подсказка
№354 учебника 2013-2022 (стр. 96):
Вспомните:
- Что такое окружность.
- Как построить средину отрезка.
№354 учебника 2023-2024 (стр. 104):
Вспомните:
- Теорему о касательной к окружности, теорему об отрезках касательных.
- Какой треугольник называют прямоугольным.
- Свойства прямоугольного треугольника.
Ответ
№354 учебника 2013-2022 (стр. 96):
Дано: точки А,В,С.
Построить: окружность, на которой лежат точки А,В,С.
Построение:

Ответ: если точки не лежат на одной - одно решение, если точки лежат на одной прямой - решения нет.
Пояснения:
Ставим точки А, В и С, с помощью линейки соединяем точки А и В, А и С, В и С.
Далее находим середины получившихся отрезков АВ, АС, ВС, т.е. строим к ним серединные перпендикуляры. Для того, чтобы построить серединный перпендикуляр к отрезку АВ, строим с помощью циркуля две окружности радиуса АВ с центрами в точках А и В (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Для того, чтобы построить серединный перпендикуляр к отрезку АС, строим две окружности радиуса АС с центрами в точках А и С (полностью окружности строить необязательно, смотри выделенное фиолетовым и коричневым цветом). Для того, чтобы построить серединный перпендикуляр к отрезку ВС, строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное красным и оранжевым цветом).
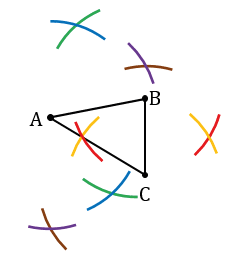
Получаем, что для каждого из отрезков, окружности пересекаются в паре точек. Проводим с помощью линейки через каждую из этих пар точек прямые 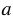 ,
, 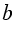 ,
, 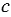 , которые будут серединными перпендикулярами к отрезкам АВ, ВС,АС соответственно.
, которые будут серединными перпендикулярами к отрезкам АВ, ВС,АС соответственно.
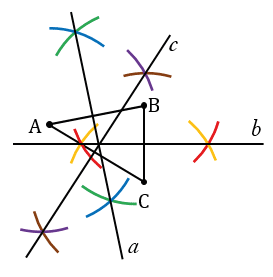
Прямые 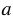 ,
, 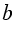 ,
,  пересекутся в точке О, данная точка будет центром искомой окружности. Строи окружность с центром в точке О радиуса ОА = ОВ = ОС.
пересекутся в точке О, данная точка будет центром искомой окружности. Строи окружность с центром в точке О радиуса ОА = ОВ = ОС.

В случае, когда точки не лежат на одной на прямой задача всегда будет иметь одно решение, когда точки лежат на одной прямой задача решения иметь не будет.
№354 учебника 2023-2024 (стр. 104):
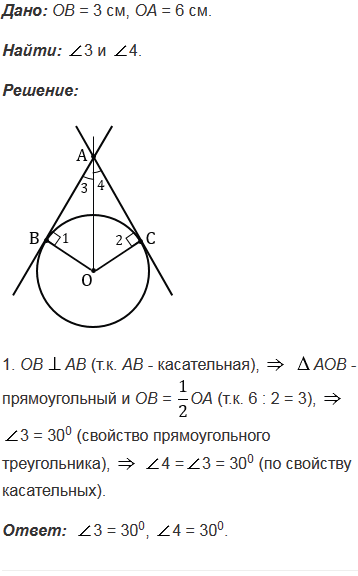

Вернуться к содержанию учебника