Задание 294 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№294 учебника 2013-2022 (стр. 88):
Постройте треугольник по двум сторонами высоте, проведенной к одной из этих сторон.
№294 учебника 2023-2024 (стр. 86):
Постройте треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла.
Подсказка
№294 учебника 2013-2022 (стр. 88):
Вспомните:
- Какая фигура называется треугольником.
- Что такое высота треугольника.
- Как построить отрезок, равный данному.
- Как построить перпендикулярные прямые.
- Что такое расстояние между параллельными прямыми.
№294 учебника 2023-2024 (стр. 86):
Вспомните:
- Какая фигура называется треугольником.
- Что такое биссектриса угла.
- Как построить угол равный данному.
- Как построить биссектрису угла.
- Как построить отрезок равный данному.
- Что такое луч.
Ответ
№294 учебника 2013-2022 (стр. 88):
Дано: отрезки Р1Q1, Р2Q2 и Р3Q3.
Построить  АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СН = Р3Q3 - высота.
АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СН = Р3Q3 - высота.
Решение:
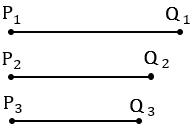
Ответ:
Пояснения:
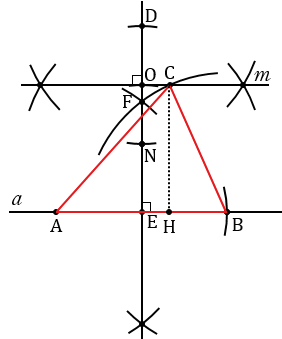
С помощью линейки проводим прямую  и на ней отложим отрезок АВ, равный отрезку P1Q1. Для этого произвольно на прямой
и на ней отложим отрезок АВ, равный отрезку P1Q1. Для этого произвольно на прямой 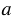 ставим точку А, с помощью циркуля измеряем отрезок P1Q1 и строим окружность с центром в точке А радиуса P1Q1 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой
ставим точку А, с помощью циркуля измеряем отрезок P1Q1 и строим окружность с центром в точке А радиуса P1Q1 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой 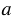 обозначаем В.
обозначаем В.
Далее с помощью циркуля измеряем длину отрезка Р2Q2 и строим окружность радиуса Р2Q2 с центром в точке В (всю окружность строить необязательно, смотри, выделенное фиолетовым цветом).
Теперь построим прямую 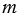 , параллельную прямой
, параллельную прямой 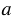 , находящиеся на расстоянии Р3Q3 друг от друга. Для этого с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В (полностью окружности строить необязательно, смотри, выделенное синим и фиолетовым цветом).
, находящиеся на расстоянии Р3Q3 друг от друга. Для этого с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В (полностью окружности строить необязательно, смотри, выделенное синим и фиолетовым цветом).
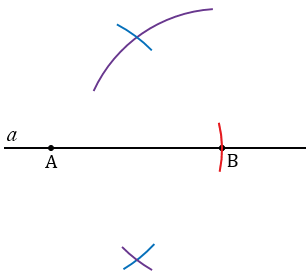
Получим две точки пересечения данных окружностей, через них с помощью линейки проводим прямую, которая пересечет прямую 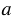 в точке Е и будет перпендикулярна к ней.
в точке Е и будет перпендикулярна к ней.
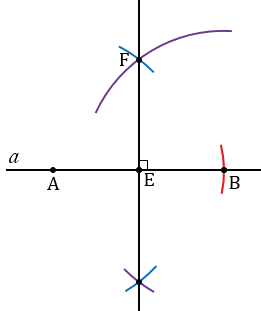
Теперь на луче ЕF отложим отрезок, равный Р3Q3. Для этого с помощью циркуля измеряем отрезок P3Q3 и строим окружность с центром в точке Е радиуса P3Q3 (всю окружность строить необязательно, смотри, выделенное зеленым цветом). Точку пересечения данной окружности с лучом ЕF обозначаем О.
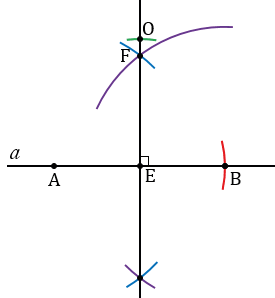
Теперь, через точку О проведем прямую 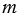 перпендикулярную к прямой ЕО, которая будет параллельна к прямой
перпендикулярную к прямой ЕО, которая будет параллельна к прямой 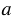 . На лучах, исходящих из точки О, с помощью циркуля откладываем равные отрезки ЕN и ED. Для этого строим окружность с центром в точке Е, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки Е (смотри выделенное красным).
. На лучах, исходящих из точки О, с помощью циркуля откладываем равные отрезки ЕN и ED. Для этого строим окружность с центром в точке Е, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки Е (смотри выделенное красным).
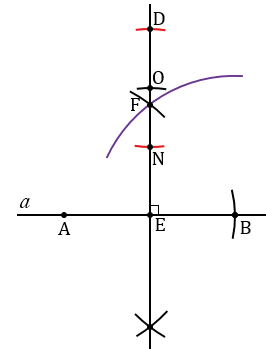
Далее с помощью циркуля строим две окружности радиуса ND с центрами в точках N и D (полностью окружности строить необязательно, смотри, выделенное синим и зеленым цветом).
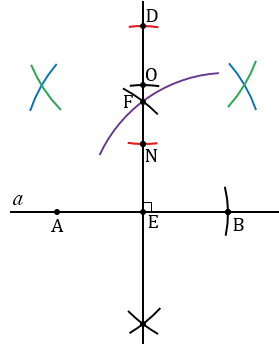
Получим две точки пересечения данных окружностей, через них с помощью линейки проводим прямую 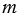 , которая будет перпендикулярна к прямой ЕО и параллельна к прямой
, которая будет перпендикулярна к прямой ЕО и параллельна к прямой 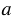 .
.
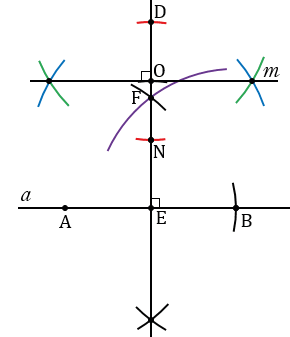
Прямая 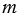 пересечет окружность с центром в точке В радиуса Р2Q2 в точке С, которая будет удалена от прямой
пересечет окружность с центром в точке В радиуса Р2Q2 в точке С, которая будет удалена от прямой 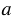 на расстояние P3Q3, т.к. прямые
на расстояние P3Q3, т.к. прямые 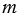 и
и 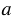 параллельны. Соединяя точку С с точками А и В с помощью линейки, получим
параллельны. Соединяя точку С с точками А и В с помощью линейки, получим 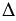 АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СН = Р3Q3 - высота.
АВС такой, что АВ = Р1Q1, ВС = Р2Q2, СН = Р3Q3 - высота.

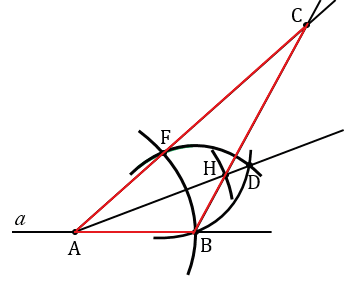
№294 учебника 2023-2024 (стр. 86):
Дано: ОЕ - сторона треугольника, 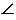 О - прилежащий к стороне ОЕ, ОК - биссектриса.
О - прилежащий к стороне ОЕ, ОК - биссектриса.
Построить: 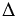 АВС, где АВ = ОЕ,
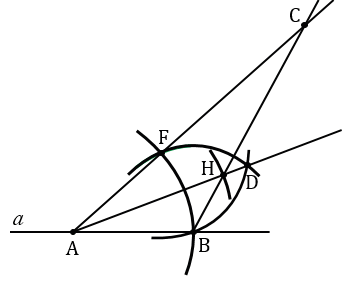
АВС, где АВ = ОЕ, 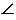 А =
А = 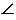 О, биссектриса АН = ОК.
О, биссектриса АН = ОК.
Решение:
Пояснения:
С помощью линейки чертим два отрезка ОЕ и ОК и угол О.
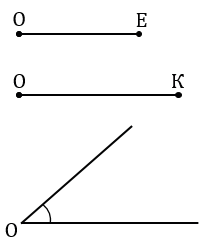
С помощью линейки проводим прямую 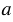 и на ней с помощью циркуля отложим отрезок АВ, равный отрезку ОЕ. Для этого произвольно на прямой
и на ней с помощью циркуля отложим отрезок АВ, равный отрезку ОЕ. Для этого произвольно на прямой 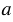 ставим точку А, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения окружности с прямой
ставим точку А, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения окружности с прямой 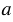 обозначаем В.
обозначаем В.
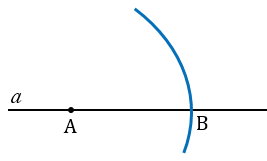
Далее строим угол ВАF равный углу О. Для этого строим с помощью циркуля окружность радиуса ОЕ с центром в вершине угла О (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла О обозначаем N и Р.
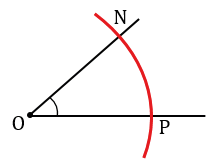
С помощью циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное зеленым цветом). Точку пересечения данной окружности с окружностью радиуса ОЕ с центром в точке А обозначаем F.
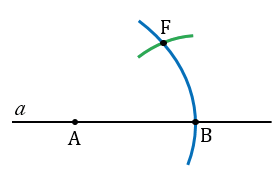
Далее, проводим луч АF с помощью линейки.
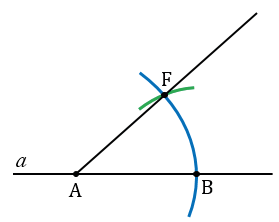
Теперь строим биссектрису угла ВАF. Для этого с помощью циркуля строим две окружности одинакового радиуса ВF с центрами в точках В и F (полностью окружности строить не обязательно, смотри выделенное красным). Точку пересечения данных окружностей обозначим D.
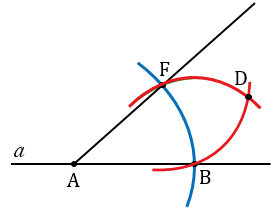
Проводим с помощью линейки луч АD - биссектрису угла ВАF.
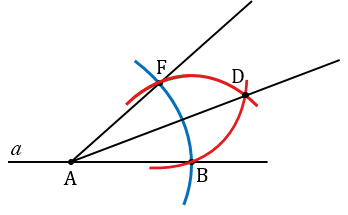
На луче АD откладываем отрезок АН, равный отрезку ОК. Для этого с помощью циркуля строим окружность с центром в точке А радиуса ОК (всю окружность строить необязательно, смотри, выделенное фиолетовым цветом). Точку пересечения данной окружности с лучом АD обозначаем Н.
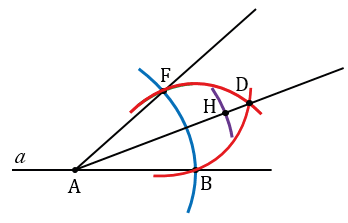
Далее, с помощью линейки проводим луч ВН. Точку пересечения лучей АF и BH обозначаем С.
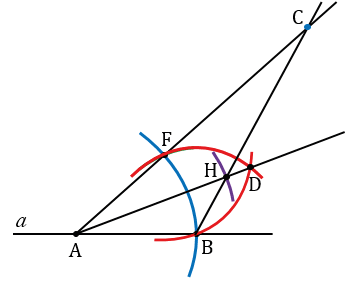
Получаем треугольник АВС, в котором по построению АВ = ОЕ, АН = ОК - биссектрисы углов О и А,  О =
О =  А, следовательно, треугольник АВС - искомый.
А, следовательно, треугольник АВС - искомый.
Вернуться к содержанию учебника