Упражнение 353 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 108

а) \((x^2 + 17)(x - 6)(x + 2) < 0\)

\(x^2 + 17 > 0\) для всех \(x\), тогда

\((x - 6)(x + 2) < 0\)

\((x - 6)(x + 2) = 0\)

\(x - 6=0\)  или  \(x + 2 = 0\)

\(x = 6\)                  \(x = -2\)

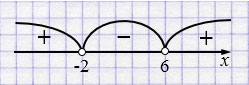
Ответ: \(x \in (-2;6)\).

б) \((2x^2 + 1)x(x - 4) > 0\)

\(2x^2 + 1 > 0\) для всех \(x\), тогда

\(x(x - 4) > 0\)

\(x(x - 4) = 0\)

\(x = 0\)  или  \( x - 4 = 0\).

                     \(x = 4\)

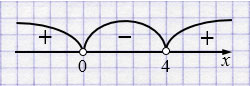
Ответ: \(x \in (-\infty; 0) \cup (4; +\infty)\)

в) \((x - 1)^2(x - 24) < 0\)

\((x - 1)^2(x - 24) = 0\)

\(x - 1 = 0\)  или  \(x - 24 = 0\)

\(x = 1\)                 \(x =24\)

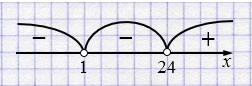
Ответ: \(x \in (-\infty;1) \cup (1;24).\)

г) \((x + 7)(x - 4)^2(x - 21) > 0\)

или \(x + 7 = 0\)

      \(x = -7\)

или \(x - 4 = 0\)

       \(x = 4\)

или \(x - 21 =0\)

       \(x = 21\)

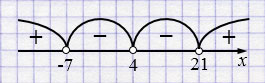
Ответ: \(x \in (-\infty; -7) \cup (21; +\infty)\).

Пояснения:

Выражения \(x^2+17\), \(2x^2+1\) всегда принимают положительные значения, поэтому на знак произведения никак не влияют и их можно не учитывать.

Выражения \((x-1)^2\), \((x-4)^2\) принимают только неотрицательные значения, поэтому на знак произведения они никак не влияют, но при строгих неравенствах, значения \(x\), при которых эти выражения равны нулю, исключаем (точки, им соответствующие на координатной прямой, делаем "выколотыми"), при этом при переходе через эти точки смены знака не происходит.

При решении неравенств используем метод интервалов.

Метод интервалов применяется к произведению вида \((x-a)(x-b)\dots\).

Находим нули каждого множителя — это точки, в которых знак выражения меняется.

Отмечаем точки на числовой прямой и определяем знак выражения на каждом интервале. Достаточно определить знак на одном интервале, а на остальных расставить знаки так, чтобы они чередовались. Чтобы определить знак на одном из интервалов, нужно взять какое-нибудь значение из рассматриваемого интервала и определить знак функции при этом значении.

Если знак требуется «>0» — берём интервалы со знаком "+", без корней; если «<0» — интервалы со знаком "–", без корней; если «≥0» — интервалы со знаком "+" и включаем корни; если «≤0» — интервалы со знаком "–" и включаем корни.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

У \(+\infty\) и \(-\infty\) при записи промежутка скобка всегда круглая.