Упражнение 1080 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1080 учебника 2023-2025 (стр. 240):
Постройте график функции, заданной формулой:
а) \(f(x)=1,5-3x\);
б) \(f(x)=4,5x\);
в) \(f(x)=\dfrac{10}{x}\);
г) \(f(x)=-\dfrac{1}{x}\).
Укажите область определения и множество значений функции.
№1080 учебника 2013-2022 (стр. 249):
Преобразуйте выражение так, чтобы оно не содержало степеней с отрицательными показателями:
а) \(\dfrac{a m^{-2}}{a^{-1} b}\);
б) \(\dfrac{(a+b)b}{b^{-1}(a-b)}\);
в) \(\dfrac{2a^{-1}b^{2}}{(a+b)^{-2}}\).
Подсказка
№1080 учебника 2023-2025 (стр. 240):
№1080 учебника 2013-2022 (стр. 249):
Вспомните:
- Степень с целым отрицательным показателем.
- Свойства степени с целым показателем.
- Взаимно обратные числа.
Ответ
№1080 учебника 2023-2025 (стр. 240):
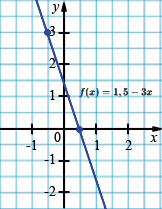
а) \(f(x)=1,5-3x\)
\(D=(- \infty; +\infty); E=(- \infty; +\infty).\)
| \(x\) | -0,5 | 0,5 |
| \(y\) | 3 | 0 |
б) \(f(x)=4,5x\).
\(D=(- \infty; +\infty); E=(- \infty; +\infty).\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | 9 |

в) \(f(x)=\dfrac{10}{x}\)
\(D=(- \infty; 0)\cup(0; +\infty);\)
\(E=(- \infty; 0)\cup(0; +\infty).\)
| \(x\) | -1 | -2 | -2,5 | -4 | -5 | -10 |
| \(y\) | -10 | -5 | -4 | -2,5 | -2 | -1 |
| \(x\) | 1 | 2 | 2,5 | 4 | 5 | 10 |
| \(y\) | 10 | 5 | 4 | 2,5 | 2 | 1 |

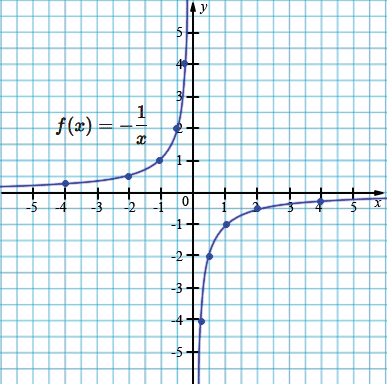
г) \(f(x)=-\dfrac{1}{x}\).
\(D=(- \infty; 0)\cup(0; +\infty);\)
\(E=(- \infty; 0)\cup(0; +\infty).\)
| \(x\) | -4 | -2 | -1 | -0,5 | -0,25 |
| \(y\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(x\) | 4 | 2 | 1 | 0,5 | 0,25 |
| \(y\) | -0,25 | -0,5 | -1 | -2 | -4 |
Пояснения:
1) Для линейных функций \(y=kx+b\) область определения и множество значений — все действительные числа.
2) Для дробно-рациональных функций вида \(\dfrac{a}{x}\) исключается \(x=0\), а значения функции также не равны нулю.
3) Графики: а), б) — прямые; в), г) — гиперболы.
№1080 учебника 2013-2022 (стр. 249):
а) \( \dfrac{a m^{-2}}{a^{-1} b} = \dfrac{aa}{bm^{2}} =\dfrac{a^2}{bm^{2}}. \)
б) \( \dfrac{(a+b)b}{b^{-1}(a-b)} = \dfrac{(a+b)bb}{(a-b)} =\)
\(=\dfrac{b^{2}(a+b)}{a-b}. \)
в) \( \dfrac{2a^{-1}b^{2}}{(a+b)^{-2}} = \dfrac{2b^{2}(a+b)^{2}}{a}.\)
Пояснения:
Использованы свойства степеней:
\( a^{-n} = \dfrac{1}{a^{n}}\), то есть число с отрицательной степенью, стоящее в числителе, переносится в знаменатель с положительной степенью, а число с отрицательной степенью, стоящее в знаменателе, переносится в числитель с положительной степенью.
\(a^ma^n = a^{m+n}\).
Вернуться к содержанию учебника