Упражнение 899 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 201

\(A = \{16, 25, 36, 49, 64, 81\}. \)

\( B = \{16, 32, 48, 64, 80, 96\}. \)

\[ A \cap B = \{16, 64\}. \]

\[ A \cup B = \{16, 25, 32, 36, 48, 49, 64, 80, 81, 96\}. \]

Пояснения:

1) Квадраты натуральных чисел от 4 до 9 дают все двузначные квадраты.

2) Кратные 16 в пределах двузначных чисел находятся последовательным умножением: \(16 \cdot 1, 16 \cdot 2, \dots, 16 \cdot 6.\)

3) Пересечение множеств (\(\cap\)) — элементы, которые встречаются и в \(A\), и в \(B\). Объединение множеств (\(\cup\)) — все элементы, которые встречаются хотя бы в одном из множеств.

а) \( \begin{cases} x-4 < 8,\\ 2x+5 < 13,\\ 3-x>1 \end{cases} \)

\( \begin{cases} x < 8 + 4,\\ 2x < 13 - 5,\\ -x>1 - 3 \end{cases} \)

\( \begin{cases} x < 12,\\ 2x < 8,  / : 2\\ -x> -2  / : (-1) \end{cases} \)

\( \begin{cases} x < 12,\\ x < 4, \\ x < 2 \end{cases} \)

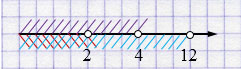
Ответ: \((-\infty; 2)\).

б) \( \begin{cases} 2x-1 < x + 3,\\ 5x-1 > 6-2x,\\ x-5 < 0 \end{cases} \)

\( \begin{cases} 2x-x < 3 + 1,\\ 5x+2x > 6+1,\\ x < 5 \end{cases} \)

\( \begin{cases} x < 4,\\ 7x > 7,  / : 7 \\ x < 5 \end{cases} \)

\( \begin{cases} x < 4,\\ x > 1, \\ x < 5 \end{cases} \)

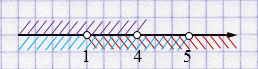
Ответ: \((1; 4)\).

Пояснения:

Чтобы решить систему неравенств, нужно найти пересечение решений всех неравенств системы, то есть найти множество чисел, которое является одновременно решением каждого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.