Упражнение 1162 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1162 учебника 2023-2025 (стр. 229):
Пересекает ли график уравнения
\(y - x^2 = 9\):
а) ось \(x\); б) ось \(y\)?
При положительном ответе укажите координаты точек пересечения.
№1162 учебника 2013-2022 (стр. 228):
Решите графически систему уравнений:
а) \( \begin{cases} y + 3x = 0,\\ x - y = 4,\\ x + y = -2; \end{cases} \)
б) \( \begin{cases} x + y = 1,\\ y - x = 3,\\ 2x + y = 0. \end{cases} \)
Подсказка
№1162 учебника 2023-2025 (стр. 229):
Вспомните:
- Уравнение с двумя переменными, его график и свойства.
- Координаты точки.
- Степень с натуральным показателем.
- Умножение рациональных чисел.
№1162 учебника 2013-2022 (стр. 228):
Вспомните:
- Графический метод решения систем уравнений с двумя переменными.
- Уравнения с двумя переменными, их свойства.
- График линейной функции.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№1162 учебника 2023-2025 (стр. 229):
\(y - x^2 = 9\):
а) С осью \(x\): \(y=0\).
\( 0 - x^2 = 9 \)
\(- x^2 = 9 \) /\(\times(-1)\)
\(x^2 = -9 \) - не имеет корней, значит, график с осью \(x\) не пересекается.
б) C осью \(y\): \(x=0\).
\( y - 0^2 = 9 \)
\(y = 9 \)
\((0;9)\) - точка пересечения с осью \(y\).
Ответ: а) график не пересекает ось \(x\); б) график пересекает ось \(y\) в точке \((0;9)\).
Пояснения:
– Чтобы найти пересечение графика с осью \(x\), ставят \(y=0\) и решают полученное уравнение по \(x\).
– Если полученное уравнение корней не имеет, пересечения не происходит.
– Для пересечения с осью \(y\) берут \(x=0\) и решают по \(y\).
– В нашем случае точка \((0;9)\) — единственная точка пересечения с осью \(y\).
№1162 учебника 2013-2022 (стр. 228):
а) \( \begin{cases} y + 3x = 0,\\ x - y = 4,\\ x + y = -2; \end{cases} \)
\( \begin{cases} y = -3x,\\ y = x - 4,\\ y = -x - 2; \end{cases} \)
\(y = -3x\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | -6 |
\(y = x - 4\)
| \(x\) | 0 | 2 |
| \(y\) | -4 | -2 |
\(y = -x - 2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | -4 |
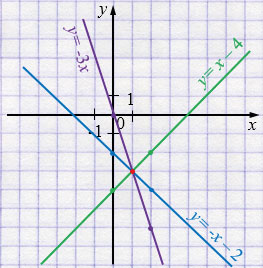
Ответ: \((1;\,-3)\).
б) \( \begin{cases} x + y = 1,\\ y - x = 3,\\ 2x + y = 0. \end{cases} \)
\( \begin{cases} y = 1 - x,\\ y = 3 + x,\\ y = -2x. \end{cases} \)
\(y = 1 - x\)
| \(x\) | 0 | 3 |
| \(y\) | 1 | -2 |
\(y = x + 3\)
| \(x\) | 0 | -3 |
| \(y\) | 3 | 0 |
\(y = -2x\)
| \(x\) | 0 | 2 |
| \(y\) | 0 | -4 |
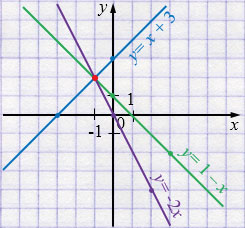
Ответ: \((-1;\,2)\).
Пояснения:
– Графически система уравнений с двумя переменными задаёт пересечение прямых на плоскости.
– Для каждой прямой удобно записать уравнение в явном виде \(y = kx + b\). Для построения прямой достаточно отметить две точки.
– В обоих случаях все три прямые проходят через одну единственную точку, что и является решением системы.
Вернуться к содержанию учебника