Упражнение 775 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

1) \(1 - \tfrac16 = \tfrac66 - \tfrac16 = \tfrac56 \) - расстояния между А и В проедет второй автобус за 3,5 ч.

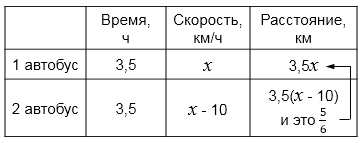
2) Составим уравнение:

\( 3,5(x - 10) = \tfrac56 \cdot 3,5x\)    / \( : 3,5\)

\(x - 10 = \tfrac56\,x \)    / \(\times 6\)

\( 6(x - 10) = 5x \)

\(6x - 60 = 5x \)

\(6x - 5x = 60 \)

\(x = 60\ \text{км/ч} \) - скорость первого автобуса.

3) \( x - 10 = 60 - 10 = 50\ \text{км/ч} \) - скорость второго автобуса.

4) \(3,5x = 3,5 \cdot 60 = 210\ \text{км}. \)

Ответ: скорость первого автобуса 60 км/ч, второго - 50 км/ч, расстояние от A до B равно 210 км.

Пояснения:

Использованные правила:

1) Формула движения: \(S = v\,t\) - чтобы найти расстояние, нужно скорость умножить на время.

2) Если автобус до прибытия отстает на \(\tfrac16\) пути, он прошёл \(\tfrac56\) пути.

3) Чтобы найти дробь от числа, нужно число умножить на эту дробь.

4) Свойство уравнений: корни уравнения не изменяются, если его левую и правую части умножить или разделить на одно и то же число.

5) Перенос подобных членов из одной части уравнения в другую со сменой знака.

\(A + C= B + D\), то

\(A - D = B - C\).

6) Приведение подобных членов

\(ka + la = (k + l)a\).

Пояснения по шагам:

— Вводим переменную \(x\) для скорости быстрого автобуса, медленный идёт на 10 км/ч медленнее.

— За \(3,5\) ч быстрый поезд проходит весь путь, равный \(3,5x\).

— За \(3,5\) ч медленный поезд проходит весь путь, равный \(3,5(x - 10)\), что также  составляет \(\tfrac56\) всего пути, то есть \(\tfrac56 \cdot 3,5x\) , поэтому можем составить уравнение:

\( 3,5(x - 10) = \tfrac56 \cdot 3,5x\)

— Решив полученное уравнение, находим \(x=60\).

— Затем вычисляем скорость медленного \(50\) км/ч и подставляем \(x\) в выражение для расстояния между пунктами А и В \(3,5x\), получая \(210\) км.

\(\overline{abc}=100a + 10b + c\)

\(\overline{cba}=100c + 10b + a\).

\(\overline{abc} - \overline{cba} =\)

\(=(100a + 10b + c) - (100c + 10b + a) =\)

\(=100a + \cancel{10b} + c - 100c - \cancel{10b} - a =\)

\(=(100a - a) + (100c - c) =\)

\(=99a - 99c = 99\,(a - c) =\)

\(=11 \cdot 9\,(a - c) \) - делится на \(11\).

Пояснения:

1. Представление трёхзначного числа: число \(\overline{abc}\) с цифрами \(a\), \(b\), \(c\) равно \(100a + 10b + c\).

2. Разность выражений: при вычитании сократились противоположные слагаемые \(10b\), что дало

\(100a - 100c + c - a=\)

\(=(100a - a) + (100c - c) =\)

\(=99a - 99c\)

3. Вынесение общего множителя:

\(99a - 99c = 99(a-c)\).

4. Делимость числа 99 на 11:

\(99 = 9 \cdot 11\), поэтому

\(99(a - c)=11 \cdot 9\,(a - c)\) кратно 11.

Итак, разность любых чисел \(\overline{abc}\) и \(\overline{cba}\) делится на \(11\).