Упражнение 668 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№668 учебника 2023-2025 (стр. 142):
Решите графически уравнение
\[x^2 = 6 - x.\]
№668 учебника 2013-2022 (стр. 144):
Вынесите за скобки общий множитель:
а) \(3a^3 - 15a^2b + 5ab^2\);
б) \(20x^4 - 25x^2y^2 - 10x^3\);
в) \(-6am^2 + 9m^3 - 12m^4\);
г) \(12a^2b - 18ab^2 - 30ab^3\);
д) \(4ax^3 + 8a^2x^2 - 12a^3x\);
е) \(-3x^4y^2 - 6x^2y^2 + 9x^2y^4\).
Подсказка
№668 учебника 2023-2025 (стр. 142):
Вспомните:
№668 учебника 2013-2022 (стр. 144):
Ответ
№668 учебника 2023-2025 (стр. 142):
\(y = x^2\)
| 0 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | |
| 0 | 1 | 1 | 4 | 4 | 9 | 9 | 16 | 16 |
\(y = 6 - x\)
| 0 | 2 | |
| 6 | 4 |
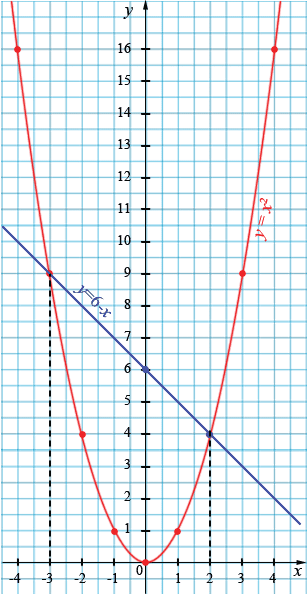
\( x = 2 \) и \(x = -3\).
Ответ: \(x = 2\) и \(x = -3\).
Пояснения:
1) Графический метод состоит в нахождении точек пересечения графиков функций \(y = f(x)\) и \(y = g(x)\), где уравнение \(f(x) = g(x)\).
2) В нашем случае \(f(x) = x^2\) (ветви параболы вверх, вершина в начале координат) и \(g(x) = 6 - x\).
3. Эти графики пересекаются в двух точках. Абсциссы точек пересечения графиков являются теми значениями переменной \(x\), при которых выражения \(x^2\) и \(6-x\) принимают равные значения. Значит, абсциссы точек пересечения являются корнями уравнения \(x^2=6-x.\)
4) Из рисунка видно, что это уравнение имеет корни: \(\;2\) и \(-3\).
№668 учебника 2013-2022 (стр. 144):
а) \(3a^3 - 15a^2b + 5ab^2 = \)
\(=a\bigl(3a^2 - 15ab + 5b^2\bigr)\).
б) \(20x^4 - 25x^2y^2 - 10x^3 =\)
\(=5x^2\bigl(4x^2 - 5y^2 - 2x\bigr)\).
в) \(-6am^2 + 9m^3 - 12m^4 =\)
\(=3m^2\bigl(-2a + 3m - 4m^2\bigr)\).
г) \(12a^2b - 18ab^2 - 30ab^3 =\)
\(=6ab\bigl(2a - 3b - 5b^2\bigr)\).
д) \(4ax^3 + 8a^2x^2 - 12a^3x =\)
\(=4ax\bigl(x^2 + 2ax - 3a^2\bigr)\).
е) \(-3x^4y^2 - 6x^2y^2 + 9x^2y^4 =\)
\(=-3x^2y^2\bigl(x^2 + 2 - 3y^2\bigr)\).
Пояснения:
Использованные правила и приёмы:
1) Распределительный закон:
\[a(b +c+d) =ab+ac+ad\]
2) Обратный распределительный закон (вынос общего множителя):
\[ab+ac+ad =a(b +c+d)\]
3) Свойство наибольшего общего делителя коэффициентов и минимальной степени переменной.
В каждом случае:
– нашли наибольший числовой общий делитель коэффициентов,
– определили минимальную степень каждой переменной,
– вынесли полученный общий множитель за скобку,
– внутри скобок записали частное каждого члена исходного выражения на этот множитель.
Вернуться к содержанию учебника