Упражнение 591 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 131
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№591 учебника 2023-2025 (стр. 131):
Докажите, что многочлен 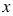 2 +
2 + 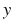 2 + 1 при любых значениях
2 + 1 при любых значениях 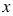 и
и 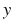 принимает положительные значения.
принимает положительные значения.
№591 учебника 2013-2022 (стр. 131):
Докажите, что:
а) сумма двух последовательных нечетных чисел кратна 4;
б) сумма четырех последовательных нечетных чисел кратна 8.
Подсказка
№591 учебника 2023-2025 (стр. 131):
Вспомните:
- Многочлены.
- Степень с натуральным показателем.
- Умножение рациональных чисел.
- Сравнение рациональных чисел.
№591 учебника 2013-2022 (стр. 131):
Вспомните:
- Четные и нечетные числа.
- Сложение и вычитание многочленов.
- Раскрытие скобок, подобные слагаемые.
- Свойства умножения.
- Кратные числа.
Ответ
№591 учебника 2023-2025 (стр. 131):
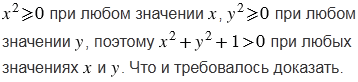
№591 учебника 2013-2022 (стр. 131):

Пояснения:
При доказательстве используем свойство умножения, согласно которому произведение делится на какое-либо число, если в произведении хотя бы один из множителей делится на это число.
Нечетные числа - это числа, которые не делятся на 2. Два последовательных нечетных числа отличаются друг от друга на 2, то есть каждое следующее нечетное число на 2 больше предыдущего.
При раскрытии скобок помним, если перед скобками стоит знак "+", то можно опустить скобки и этот знак "+", сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком "+".
После раскрытия скобок приводим подобные слагаемые (в решении выделены одинаковым цветом). Затем, используя распределительное свойство выносим одинаковый множитель за скобки, который делится на то число, которое нам дано, а это говорит о том, что и все произведение делится на это числа, то есть рассматриваемая сумма кратна этому числу.
Вернуться к содержанию учебника