Упражнение 467 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№467 учебника 2023-2025 (стр. 109):
Какой цифрой может оканчиваться:
а) квадрат натурального числа;
б) четвертая степень натурального числа?
№467 учебника 2013-2022 (стр. 111):
Выполните умножение:
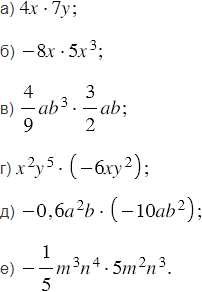
Подсказка
№467 учебника 2023-2025 (стр. 109):
Вспомните:
- Какие числа называют натуральными.
- Степень с натуральным показателем.
- Свойства степени.
№467 учебника 2013-2022 (стр. 111):
Вспомните:
- Одночлены.
- Умножение одночленов.
- Свойства степени с натуральным показателем.
- Умножение десятичных дробей.
- Умножение обыкновенных дробей.
- Умножение рациональных чисел.
Ответ
№467 учебника 2023-2025 (стр. 109):
а) 02 = 0; 12 = 1;
22 = 4; 32 = 9;
42 = 16; 52 = 25;
62 = 36; 72 = 49;
82 = 64; 92 = 81;
Ответ: квадрат натурального числа может оканчиваться цифрами: 0; 1; 4; 5; 6; 9.
б) 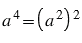
02 = 0; 12 = 1;
42 = 16; 52 = 25;
62 = 36; 92 = 81.
Ответ: четвертая степень натурального числа может оканчиваться цифрами: 0; 1; 5; 6.
Пояснения:
а) Чтобы узнать, какой цифрой может оканчиваться квадрат натурального числа, нужно возвести все цифры в квадрат и посмотреть, чем оканчиваются полученные числа.
б) Чтобы узнать, какой цифрой оканчивается четвертая степень числа, не нужно возводить все цифры в четвертую степень, достаточно возвести в квадрат цифры, которыми может оканчиваться вторая степень натурального числа, так как 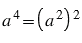 , и посмотреть, чем оканчиваются полученные числа.
, и посмотреть, чем оканчиваются полученные числа.
№467 учебника 2013-2022 (стр. 111):

Пояснения:
Одночлены - это выражения, представляющие собой произведение чисел, переменных и их степеней. При умножении одночленов и возведении одночлена в степень используются правило умножения степеней с одинаковыми основаниями и правило возведения степени в степень. При этом получается одночлен, который обычно представляют в стандартном виде.
Вернуться к содержанию учебника