Задание 6.350 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.350 учебника 2023-2024 (стр. 139):
От автовокзала в 12 ч 25 мин отошел автобус, а в 14 ч 40 мин в противоположном направлении отошел другой автобус. Какое расстояние будет между автобусами через 2,4 ч после выезда второго автобуса, если скорость первого автобуса 72,4 км/ч, а скорость второго - 65,8 км/ч?
№6.350 учебника 2021-2022 (стр. 124):
Расстояние между двумя пристанями теплоход прошел по течению реки за 1,8 ч, а затем вернулся обратно. Сколько времени затратил теплоход на обратный путь, если его собственная скорость равна 24 км/ч, а скорость течения - 2,4 км/ч?
Подсказка
№6.350 учебника 2023-2024 (стр. 139):
Вспомните:
- Задачи на движение.
- Сложение десятичных дробей.
- Умножение десятичных дробей.
- Единицы измерения времени.
- Обыкновенные дроби.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
№6.350 учебника 2021-2022 (стр. 124):
Вспомните:
- Задачи на движение.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Деление десятичных дробей.
Ответ
№6.350 учебника 2023-2024 (стр. 139):
1) 14 ч 40 мин - 12 ч 25 мин =
= 2 ч 15 мин = 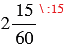 ч =
ч = 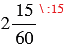 ч =
ч =
= 2,25 ч - время в пути первого автобуса до выхода второго.
2) 2,25 + 2,4 = 4,65 (ч) - был в пути первый автобус.
3) 72,4 • 4,65 = 336,66 (км) - проехал первый автобус.
| × | 7 | 2 | 4 | |||
| 4 | 6 | 5 | ||||
| + | 3 | 6 | 2 | 0 | ||
| 4 | 3 | 4 | 4 | |||
| 2 | 8 | 9 | 6 | |||
| 3 | 3 | 6 | 6 | 6 | 0 |
4) 65,8 • 2,4 = 157,92 (км) - проехал второй автобус.
| × | 6 | 5 | 8 | ||
| 2 | 4 | ||||
| + | 2 | 6 | 3 | 2 | |
| 1 | 3 | 1 | 6 | ||
| 1 | 5 | 7 | 9 | 2 |
5) 336,66 + 157,92 = 494,58 (км)
| + | 3 | 3 | 6 | , | 6 | 6 |
| 1 | 5 | 7 | , | 9 | 2 | |
| 4 | 9 | 4 | , | 5 | 8 |
Ответ: 494,58 км будет между автобусами.
Пояснения:
От автовокзала в 12 ч 25 мин отошел первый автобус, значит, в 14 ч 40 мин он был уже в пути:
14 ч 40 мин - 12 ч 25 мин = 2 ч 15 мин =
= 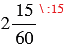 ч =
ч = 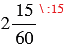 ч = 2,25 ч.
ч = 2,25 ч.
При выполнении преобразований мы учли то, что 1 ч = 60 мин. Чтобы преобразовать обыкновенную дробь в десятичную, числитель разделили на знаменатель.
Первый автобус до выхода второго был в пути 2,25 ч, а вместе они были в пути 2,4 ч, значит, всего первый автобус был в пути:
2,25 + 2,4 = 4,65 (ч).
Чтобы найти расстояние, нужно скорость движения умножить на время.
Скорость первого автобуса 72,4 км/ч, значит, за 4,65 ч первый автобус проехал:
72,4 • 4,65 = 336,66 (км).
Скорость второго автобуса 65,8 км/ч, значит, за 2,4 ч второй автобус проехал:
65,8 • 2,4 = 157,92 (км).
Два автобуса выехали с автовокзала в противоположных направлениях, первый автобус проехал 336,66 км, а второй - 157,92 км, значит, расстояние между автобусами:
336,66 + 157,92 = 494,58 (км).
Правила вычислений с десятичными дробями смотрите в подсказке.
№6.350 учебника 2021-2022 (стр. 124):
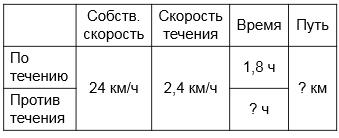
1) 24 + 2,4 = 26,4 (км/ч) -скорость по течению реки.
2) 26,4 • 1,8 = 47,52 (км) - расстояние между пристанями.
| × | 2 | 6 | 4 | |
| 1 | 8 | |||
| + | 2 | 1 | 1 | 2 |
| 2 | 6 | 4 | ||
| 4 | 7 | 5 | 2 |
3) 24 - 2,4 = 21,6 (км/ч) - скорость против течения.
| • | ||||
| - | 2 | 4 | , | 0 |
| 2 | , | 4 | ||
| 2 | 1 | , | 6 |
4) 47,52 : 21,6 = 2,2 (ч)
| - | 4 | 7 | 5 | 2 | 2 | 1 | 6 | ||||||||||
| 4 | 3 | 2 | 2 | 2 | |||||||||||||
| - | 4 | 3 | 2 | ||||||||||||||
| 4 | 3 | 2 | |||||||||||||||
| 0 |
Ответ: за 2,2 ч затратил теплоход на обратный путь.
Пояснения:
Собственная скорость теплохода равна 24 км/ч, а скорость течения - 2,4 км/ч, значит, скорость теплохода по течению реки:
24 + 2,4 = 26,4 (км/ч).
Чтобы найти расстояние, нужно скорость движения умножить на время.
Скорость теплохода по течению реки 26,4 км/ч, значит, за 1,8 ч теплоход проплыл:
26,4 • 1,8 = 47,52 (км).
Следовательно, расстояние между пристанями 47,52 км.
Собственная скорость теплохода равна 24 км/ч, а скорость течения - 2,4 км/ч, значит, скорость теплохода против течения реки:
24 - 2,4 = 21,6 (км/ч).
Чтобы найти время, нужно расстояние разделить на скорость движения.
Скорость теплохода на обратном пути (против течения) 21,6 км/ч, расстояние между пристанями 47,53 км, значит, время, за которое теплоход преодолеет это расстояние:
47,52 : 21,6 = 2,2 (ч).
Правила вычислений с десятичными дробями смотрите в подсказке.
Вернуться к содержанию учебника