Задание 6.346 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.346 учебника 2023-2024 (стр. 139):
Найдите четыре значения 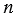 , при которых неравенство будет верным:
, при которых неравенство будет верным:
а) 4,3 < 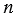 < 4,7;
< 4,7;
б) 5,5 < 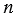 < 5,7;
< 5,7;
в) 0,003 < 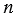 < 0,004;
< 0,004;
г) 0,07 < 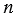 < 0,071.
< 0,071.
№6.346 учебника 2021-2022 (стр. 123):
Сравните, не вычисляя, значение выражений:
а) 78 • 0,16 и (78 • 16) : 100;
б) 0,037 • 0,3 и (37 • 3) : 10 000.
Объясните полученный ответ.
Подсказка
№6.346 учебника 2023-2024 (стр. 139):
№6.346 учебника 2021-2022 (стр. 123):
Вспомните:
- Сравнение десятичных дробей.
- Деление десятичных дробей.
- Свойства деления.
Ответ
№6.346 учебника 2023-2024 (стр. 139):
а) 4,3 < 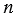 < 4,7
< 4,7
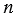 = 4,4; 4,5; 4,6; 4,65.
= 4,4; 4,5; 4,6; 4,65.
б) 5,5 < 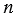 < 5,7
< 5,7
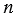 = 5,56; 5,59; 5,6; 5,67.
= 5,56; 5,59; 5,6; 5,67.
в) 0,003 < 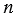 < 0,004
< 0,004
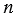 = 0,0031; 0,0034, 0,0036; 0,0039.
= 0,0031; 0,0034, 0,0036; 0,0039.
г) 0,07 < 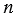 < 0,071
< 0,071
 = 0,0703; 0,0705; 0,0707; 0,0709.
= 0,0703; 0,0705; 0,0707; 0,0709.
Пояснения:
При поиске решений неравенств опираемся на правила сравнения дробей:
1) из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение);
2) чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (правило 1).
№6.346 учебника 2021-2022 (стр. 123):
а) 78 • 0,16 = (78 • 16) : 100, так как
(78 • 16) : 100=78 • (16 : 100)=78 • 0,16.
б) 0,037 • 0,3 = (37 • 3) : 10 000, так как
(37 • 3) : 10 000 = (37 • 3) : (1000 • 10) =
= (37 : 1000) • (3 : 10) = 0,037 • 0,3.
Пояснения:
При пояснении опираемся на свойства деления, согласно которым:
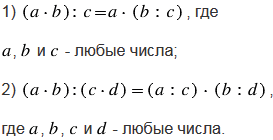
Чтобы разделить десятичную дробь на 10, 100, 1 000 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры. При это учитываем то, что любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой, т.е. у натурального числа запятую подразумеваем, но не пишем, на конце справа.
Вернуться к содержанию учебника