Задание 3.105 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 137
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№3.105 учебника 2023-2024 (стр. 137):
На рисунке 3.7 изображены два участка земли в масштабе 1 : 50 000. Найдите их действительные размеры, периметр и площадь.

№3.105 учебника 2021-2022 (стр. 137):
На рисунке 62 изображены два участка земли в масштабе 1 : 50 000. Найдите их действительные размеры, периметр и площадь.

Подсказка
№3.105 учебника 2023-2024 (стр. 137):
№3.105 учебника 2021-2022 (стр. 137):
Вспомните:
- Что называют масштабом.
- Что называют пропорцией.
- Что называют уравнением.
- Единицы измерения длины.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение десятичных дробей.
- Как найти периметр и площадь прямоугольника.
- Как найти периметр и площадь квадрата.
- Степень с натуральным показателем.
Ответ
№3.105 учебника 2023-2024 (стр. 137):
1) Первый участок.
Длина и ширина на рисунке: 3 см и 2 см.
Длина и ширина на местности: 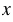 см и
см и 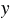 см.
см.
Масштаб: 1 : 50 000
1) 3 : 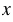 = 1 : 50 000
= 1 : 50 000
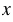 = 350 000
= 350 000
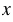 = 150 000 (см)
= 150 000 (см)
150 000 см = 1 500 м = 1,5 км - длина первого участка на местности.
2) 2 : 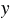 = 1 : 50 000
= 1 : 50 000
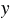 = 250 000
= 250 000
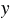 = 100 000 (см)
= 100 000 (см)
100 000 см = 1 000 м = 1 км - ширина первого участка на местности.
3) 2 • (1,5 + 1) = 2 • 2,5 = 5 (км) - периметр первого участка на местности.
4) 1,5 • 1 = 1,5 (км2)
Ответ: 1,5 км, 1 км, 5 км, 1,5 км2.
2) Второй участок.
Сторона участка на рисунке: 1,5 см.
Сторона участка на местности: 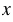 см.
см.
Масштаб: 1 : 50 000
1) 1,5 : 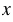 = 1 : 50 000
= 1 : 50 000
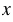 = 1,550 000
= 1,550 000
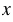 = 75 000 (см)
= 75 000 (см)
| × | 1 | 5 | ||||
| 5 | 0 | 0 | 0 | 0 | ||
| 7 | 5 | 0 | 0 | 0 | 0 |
75 000 см = 750 м - сторона второго участка на местности.
2) 4 • 750 = 3000 (м) - периметр второго участка местности.
| × | 7 | 5 | 0 |
| 4 | |||
| 3 | 0 | 0 | 0 |
3) 7502 = 750 • 750 = 562 500 (м2) - площадь второго участка на местности.
| × | 7 | 5 | 0 | |||
| 7 | 5 | 0 | ||||
| + | 3 | 7 | 5 | |||
| 5 | 2 | 5 | ||||
| 5 | 6 | 2 | 5 | 0 | 0 |
Ответ: 750 м, 3000 м, 562 500 м2.
Пояснения:
Масштабом называют отношение длины отрезка на рисунке к длине соответствующего отрезка в реальности. Расстояние на местности и длина отрезка на карте должны быть выражены одинаковыми единицами измерения.
Частное 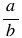 (
(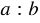 ) двух чисел
) двух чисел 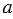 и
и 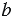 называют отношением этих чисел. Отношение показывает, во сколько раз число
называют отношением этих чисел. Отношение показывает, во сколько раз число 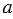 больше числа
больше числа 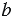 , или какую часть число
, или какую часть число 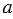 составляет от числа
составляет от числа 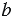 . Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
. Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
1) Первый участок.
Первый участок имеет форму прямоугольника. Длина и ширина первого участка на рисунке 3 см и 2 см соответственно. Обозначаем длину и ширину первого участка на местности (в сантиметрах) буквами 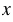 и
и 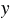 соответственно. Найдем отношение длины участка на рисунке к длине участка на местности: 3 :
соответственно. Найдем отношение длины участка на рисунке к длине участка на местности: 3 : 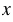 . Оно будет равно масштабу данного рисунка 1 : 50 000. Значит,
. Оно будет равно масштабу данного рисунка 1 : 50 000. Значит,
3 : 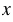 = 1 : 50 000.
= 1 : 50 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
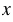 = 350 000,
= 350 000,
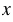 = 150 000.
= 150 000.
Значит, длина первого участка на местности равна 150 000 см, или, учитывая то, что
1 км = 1000 м = 100 000 см,
получаем, что длина первого участка на местности равна:
150 000 см = 1 500 м = 1,5 км.
Аналогично находим ширину первого участка получаем, что она равна 1 км (смотри решение выше).
Периметр прямоугольника равен удвоенной сумме его длины и ширины, тогда периметр первого участка равен:
2 • (1,5 + 1) = 2 • 2,5 = 5 (км).
Площадь прямоугольника равна произведению его длины и ширины, тогда площадь первого участка равна:
1,5 • 1 = 1,5 (км2).
2) Второй участок.
Второй участок имеет форму квадрата, сторона которого на рисунке 1,5 см. Обозначаем сторону второго участка на местности (в сантиметрах) буквой 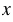 . Найдем отношение стороны участка на рисунке к стороне участка на местности: 1,5 :
. Найдем отношение стороны участка на рисунке к стороне участка на местности: 1,5 : 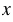 . Оно будет равно масштабу рисунка 1 : 50 000. Значит,
. Оно будет равно масштабу рисунка 1 : 50 000. Значит,
1,5 : 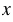 = 1 : 50 000.
= 1 : 50 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
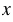 = 1,550 000,
= 1,550 000,
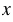 = 750 000.
= 750 000.
Значит, сторона второго участка на местности равна 75 000 см, или, учитывая то, что
1 м = 100 см,
получаем, что сторона второго участка на местности равна:
75 000 см = 750 м.
Чтобы найти периметр квадрата, нужно длину его стороны умножить на 4 (так как все стороны квадрата равны), тогда периметр второго участка равен:
4 • 750 = 3000 (м).
Площадь квадрата равна квадрату его стороны, значит, площадь второго участка равна:
7502 = 750 • 750 = 562 500 (км2).
№3.105 учебника 2021-2022 (стр. 137):
1) Первый участок.
Длина и ширина на рисунке: 5,6 см и 2,8 см.
Длина и ширина на местности: 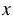 см и
см и 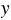 см.
см.
Масштаб: 1 : 50 000
1) 5,6 : 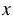 = 1 : 50 000
= 1 : 50 000
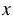 = 5,650 000
= 5,650 000
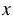 = 280 000 (см)
= 280 000 (см)
| × | 5 | 6 | ||||
| 5 | 0 | 0 | 0 | 0 | ||
| 2 | 8 | 0 | 0 | 0 | 0 | 0 |
280 000 см = 2 800 м = 2,8 км - длина первого участка на местности.
2) 2,8 : 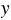 = 1 : 50 000
= 1 : 50 000
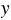 = 2,850 000
= 2,850 000
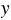 = 140 000 (см)
= 140 000 (см)
| × | 2 | 8 | ||||
| 5 | 0 | 0 | 0 | 0 | ||
| 1 | 4 | 0 | 0 | 0 | 0 | 0 |
140 000 см = 1 400 м = 1,4 км - ширина первого участка на местности.
3) 2 • (2,8 + 1,4) = 2 • 4,2 = 8,4 (км) - периметр первого участка на местности.
4) 2,8 • 1,4 = 3,92 (км2)
| × | 2 | 8 | |
| 1 | 4 | ||
| + | 1 | 1 | 2 |
| 2 | 8 | ||
| 3 | 9 | 2 |
Ответ: 2,8 км, 1,4 км, 8,4 км, 3,92 км2.
2) Второй участок.
Сторона участка на рисунке: 3,2 см.
Сторона участка на местности: 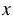 см.
см.
Масштаб: 1 : 50 000
1) 3,2 : 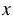 = 1 : 50 000
= 1 : 50 000
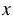 = 3,250 000
= 3,250 000
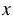 = 160 000 (см)
= 160 000 (см)
| × | 3 | 2 | ||||
| 5 | 0 | 0 | 0 | 0 | ||
| 1 | 6 | 0 | 0 | 0 | 0 | 0 |
160 000 см = 1 600 м = 1,6 км - сторона второго участка на местности.
2) 4 • 1,6 = 6,4 (км) - периметр второго участка местности.
| × | 1 | 6 |
| 4 | ||
| 6 | 4 |
3) 1,62 = 1,6 • 1,6 = 2,56 (км2) - площадь второго участка на местности.
| × | 1 | 6 | |
| 1 | 6 | ||
| + | 9 | 6 | |
| 1 | 6 | ||
| 2 | 5 | 6 |
Ответ: 1,6 км, 6,4 км, 2,56 км2.
Пояснения:
Масштабом называют отношение длины отрезка на рисунке к длине соответствующего отрезка в реальности. Расстояние на местности и длина отрезка на карте должны быть выражены одинаковыми единицами измерения.
Частное 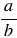 (
(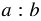 ) двух чисел
) двух чисел 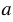 и
и 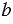 называют отношением этих чисел. Отношение показывает, во сколько раз число
называют отношением этих чисел. Отношение показывает, во сколько раз число 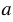 больше числа
больше числа 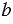 , или какую часть число
, или какую часть число 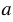 составляет от числа
составляет от числа 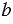 . Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
. Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
1) Первый участок.
Первый участок имеет форму прямоугольника. Длина и ширина первого участка на рисунке 5,6 см и 2,8 см соответственно. Обозначаем длину и ширину первого участка на местности (в сантиметрах) буквами 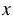 и соответственно. Найдем отношение длины участка на рисунке к длине участка на местности: 5,6 :
и соответственно. Найдем отношение длины участка на рисунке к длине участка на местности: 5,6 : 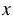 . Оно будет равно масштабу данного рисунка 1 : 50 000. Значит,
. Оно будет равно масштабу данного рисунка 1 : 50 000. Значит,
5,6 : 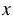 = 1 : 50 000.
= 1 : 50 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
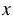 = 5,650 000,
= 5,650 000,
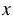 = 280 000.
= 280 000.
Значит, длина первого участка на местности равна 280 000 см, или, учитывая то, что
1 км = 1000 м = 100 000 см,
получаем, что длина первого участка на местности равна:
280 000 см = 2 800 м = 2,8 км.
Аналогично находим ширину первого участка получаем, что она равна 1.4 км (смотри решение выше).
Периметр прямоугольника равен удвоенной сумме его длины и ширины, тогда периметр первого участка равен:
2 • (2,8 + 1,4) = 2 • 4,2 = 8,4 (км).
Площадь прямоугольника равна произведению его длины и ширины, тогда площадь первого участка равна:
2,8 • 1,4 = 3,92 (км2).
2) Второй участок.
Второй участок имеет форму квадрата, сторона которого на рисунке 3,2 см. Обозначаем сторону второго участка на местности (в сантиметрах) буквой 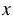 . Найдем отношение стороны участка на рисунке к стороне участка на местности: 3,2 :
. Найдем отношение стороны участка на рисунке к стороне участка на местности: 3,2 : 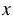 . Оно будет равно масштабу рисунка 1 : 50 000. Значит,
. Оно будет равно масштабу рисунка 1 : 50 000. Значит,
3,2 : 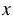 = 1 : 50 000.
= 1 : 50 000.
Чтобы найти неизвестный член полученной пропорции, используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, тогда:
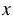 = 3,250 000,
= 3,250 000,
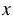 = 160 000.
= 160 000.
Значит, сторона второго участка на местности равна 160 000 см, или, учитывая то, что
1 км = 1000 м = 100 000 см,
получаем, что сторона второго участка на местности равна:
160 000 см = 1 600 м = 1,6 км.
Чтобы найти периметр квадрата, нужно длину его стороны умножить на 4 (так как все стороны квадрата равны), тогда периметр второго участка равен:
4 • 1,6 = 6,4 (км).
Площадь квадрата равна квадрату его стороны, значит, площадь второго участка равна:
1,62 = 1,6 • 1,6 = 2,56 (км2).
Вернуться к содержанию учебника