Задание 2.57 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.57 учебника 2023-2024 (стр. 51):
Найдите все общие делители чисел:
а) 20 и 70;
б) 36, 48 и 144;
в) 22 и 105.
№2.57 учебника 2021-2022 (стр. 43):
Найдите значение выражения:
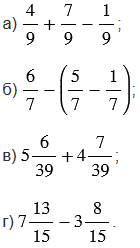
Подсказка
№2.57 учебника 2023-2024 (стр. 51):
Вспомните:
- Понятие делитель числа.
- Разложение на простые множители.
№2.57 учебника 2021-2022 (стр. 43):
Вспомните:
- Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями.
- Сложение и вычитание смешанных чисел.
- Сокращение дробей.
- Порядок выполнения действий.
- Неправильные дроби.
Ответ
№2.57 учебника 2023-2024 (стр. 51):
а) Делители числа 20: 1, 2, 4, 5, 10,20.
Делители числа 70: 1, 2, 5, 7, 10, 14, 35, 70.
Общие делители: 1, 2, 5, 10.
б) Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Делители числа 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144.
Общие делители: 1, 2, 3, 4, 6, 12.
в) Делители числа 22: 1, 2, 11, 22.
Делители числа 105: 1, 3, 5, 7, 15, 21, 35, 105.
Общие делители: 1.
Пояснения:
Делителем натурального числа n называют натуральное число, на которое n делится без остатка. Общие делители чисел - это числа, которые встречаются среди делителей всех чисел, общие делители которых необходимо найти.
№2.57 учебника 2021-2022 (стр. 43):
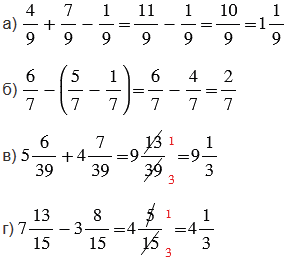
Пояснения:
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Чтобы найти сумму (разность) двух смешанных чисел, надо отдельно сложить (вычесть) их целые и дробные части.
Если при вычислениях получается сократимая дробь, то сокращаем ее (числитель и знаменатель делим на их общий делитель).
Если при вычислениях получается неправильная дробь (числитель больше знаменателя), преобразуем ее в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
В выражениях а) и б) порядок выполнения действий выбираем по следующим правилам:
1) если в выражении нет скобок и оно содержит только действия сложения и вычитания, то действия выполняют по порядку слева направо.
2) если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками.
Вернуться к содержанию учебника