Задание 541 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№541 учебника 2013-2022 (стр. 140):
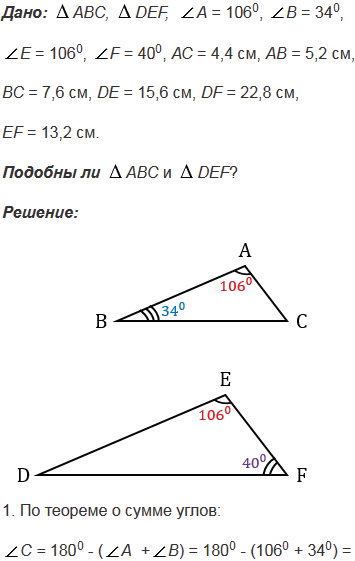
Подобны ли треугольники АВС и DEF, если 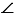 А = 1060,
А = 1060, 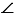 В = 340,
В = 340, 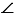 Е = 1060,
Е = 1060, 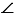 F = 400, АС = 4,4 см, АВ = 5,2 см, ВС = 7,6 см, DE = 15,6 см, DF = 22,8 см, EF = 13,2 см?
F = 400, АС = 4,4 см, АВ = 5,2 см, ВС = 7,6 см, DE = 15,6 см, DF = 22,8 см, EF = 13,2 см?
№541 учебника 2023-2024 (стр. 144):
Вырежите из бумаги два равных прямоугольных треугольника и составьте из них: а) равнобедренный треугольник; б) прямоугольник; в) параллелограмм, отличный от прямоугольника. Сравните площади полученных фигур.
Подсказка
№541 учебника 2013-2022 (стр. 140):
Вспомните:
- Какая фигура называется треугольником.
- Какие треугольники называются подобными.
- Теорему о сумме углов треугольника.
- Какие отрезки называются пропорциональными.
№541 учебника 2023-2024 (стр. 144):
Вспомните:
- Какой треугольник называется прямоугольным.
- Какой треугольник называется равнобедренным.
- Какой четырехугольник называется прямоугольником.
- Какой четырехугольник называется параллелограммом.
- Что такое площадь многоугольника, ее свойства.
Ответ
№541 учебника 2013-2022 (стр. 140):




№541 учебника 2023-2024 (стр. 144):
а) 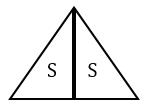
б) 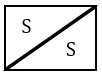
в) 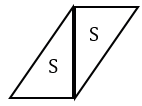
Площади полученных фигур равны (по свойству площадей).
Пояснения:
Чертим два равных прямоугольных треугольника и вырезаем их.
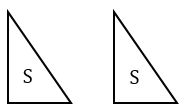
Площади данных треугольников равны, т.к. по свойству 10 площадей: равные многоугольники имеют равные площади.
а) Для того, чтобы получить равнобедренный треугольник, соединяем два прямоугольных треугольника одинаковыми катетами друг к другу.
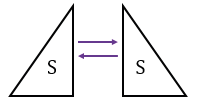
б) Для того, чтобы получить прямоугольник, соединяем два прямоугольных треугольника гипотенузами друг к другу.
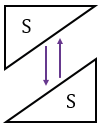
в) Для того, чтобы получить параллелограмм, соединяем два прямоугольных треугольника равными катетами друг к другу, при этом один из треугольников переворачиваем.
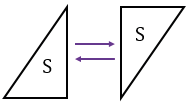
Площади полученных фигур будут равны, т.к. каждая из них составлена из двух треугольников имеющих равные площади, а по свойству 20 площадей: если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Вернуться к содержанию учебника