Задание 386 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№386 учебника 2013-2022 (стр. 105):
Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
№386 учебника 2023-2024 (стр. 111):
Подсказка
№386 учебника 2013-2022 (стр. 105):
Вспомните:
- Какая фигура называется трапецией.
- Какая точка называется серединой отрезка.
- Какие прямые называются параллельными.
№386 учебника 2023-2024 (стр. 111):
Вспомните, какие точки называют симметричными относительно прямой.
Ответ
№386 учебника 2013-2022 (стр. 105):


№386 учебника 2023-2024 (стр. 111):
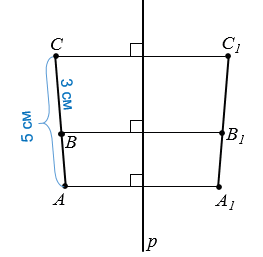
Дано: точки А1, В1, С1 симметричны точкам А, В, С, прямая р - ось симметрии, А - В - С, АС = 5 см, ВС = 3 см.
Найти: А1В1.
Решение:
1. А - В - С, 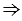 АВ = АС - ВС = 5 - 3 = 2 (см).
АВ = АС - ВС = 5 - 3 = 2 (см).
2. Точки А1, В1, симметричны точкам А, В, 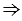 А1В1 = АВ = 2 см.
А1В1 = АВ = 2 см.
Ответ: А1В1 = 2 см.
Пояснения:
Две точки А и А1 называются симметричными относительно прямой р, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
По условию точка В лежит между точками А и С (коротко это можно записать так: А - В - С), тогда
АВ = АС - ВС = 5 - 3 = 2 (см).
Расстояния между данными точками и симметричными им точками сохраняются. Следовательно, учитывая то, что точки А1, В1, симметричны точкам А, В, имеем А1В1 = АВ = 2 см.
Вернуться к содержанию учебника