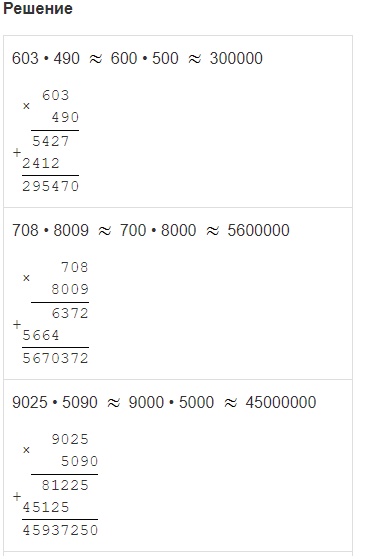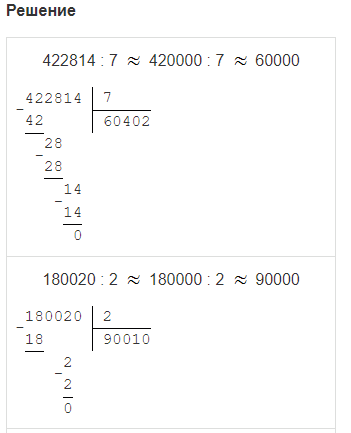Страница 29. Урок 10 - ГДЗ Математика 4 класс. Петерсон. Учебник часть 1
Вернуться к содержанию учебника
Страница 26. Урок 9 Страница 27. Урок 9 Страница 28. Урок 10 Страница 29. Урок 10 Страница 30. Урок 10 Страница 31. Урок 11 Страница 32. Урок 11
Вопрос
Задание № 3. Сделай прикидку умножения, а затем вычисли ответ:
| 603 • 490 | 708 • 8009 | 9025 • 5090 | 7103 • 703 |
Подсказка
Повтори алгоритм письменного умножения многозначных чисел.
Ответ
Вопрос
Задание № 4. Сделай прикидку деления, а затем найди частное:
| 422814 : 7 | 168024 : 3 |
| 180020 : 2 | 403500 : 5 |
| 163680 : 8 | 1600236 : 4 |
Подсказка
Повтори алгоритм письменного деления многозначных чисел.
Ответ
Вопрос
Задание № 5. За а одинаковых мячей уплатили b рублей, а за с кукол по одной цене уплатили d рублей. На сколько одна кукла в этой покупке стоит дороже одного мяча? Составь выражение и найди его значение для а = 18, b = 900, с = 16, d = 1600.
Ответ
Решение
d : с - b : а (руб.)
1600 : 16 - 900 : 18 = 50 (руб.)
Ответ: одна кукла на 50 рублей дороже одного мяча.
Пояснение
Чтобы узнать, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
Вопрос
Задние № 6.
а) В роще 240 берёз, а клёнов на 93 меньше. Сосен в ней вдвое больше, чем клёнов, а елей - в 3 раза меньше, чем сосен и берёз вместе. Сколько всего деревьев в этой роще?
б) Из леса принесли 38 грибов: белых, подосиновиков и подберёзовиков. Подберёзовиков было в 4 раза больше, чем белых, а подберёзовиков и подосиновиков вместе было 34 гриба. Сколько грибов каждого вида принесли из леса?
Подсказка
Ответ
Решение
а) 1) 240 - 93 = 147 (кл.) - в роще.
| • | • | ||
| - | 2 | 4 | 0 |
| 9 | 3 | ||
| 1 | 4 | 7 |
2) 147 • 2 = 294 (с.) - в роще.
| × | 1 | 4 | 7 |
| 2 | |||
| 2 | 9 | 4 |
3) 294 + 240 = 534 (д.) - сосен и берёз вместе.
4) 534 : 3 = 178 (ел.) - в роще.
| - | 5 | 3 | 4 | 3 | |||||||||||
| 3 | 1 | 7 | 8 | ||||||||||||
| - | 2 | 3 | |||||||||||||
| 2 | 1 | ||||||||||||||
| - | 2 | 4 | |||||||||||||
| 2 | 4 | ||||||||||||||
| 0 |
5) 534 + 178 + 147 = 859 (д.)
| + | 5 | 3 | 4 |
| 1 | 7 | 8 | |
| 1 | 4 | 7 | |
| 8 | 5 | 9 |
Ответ: 859 деревьев в этой роще.
Сколько клёнов в роще?
1) 240 - 93 = 147 (кл.)
Сколько сосен в роще?
2) 147 • 2 = 294 (с.)
Сколько сосен и берёз вместе?
3) 294 + 240 = 534 (д.)
Сколько елей в роще?
4) 534 : 3 = 178 (ел.)
Сколько всего деревьев в этой роще?
5) 534 + 178 + 147 = 859 (д.)
б) 1) 38 - 34 = 4 (гр.) - белых.
2) 4 • 4 = 16 (гр.) - подберёзовиков.
3) 34 - 16 = 18 (гр.)
Ответ: из леса принесли 4 белых гриба, 16 подберёзовиков и 18 подосиновика.
Сколько белых грибов принесли из леса?
1) 38 - 34 = 4 (гр.)
Сколько подберёзовиков принесли из леса?
2) 4 • 4 = 16 (гр.)
Сколько подосиновиков принесли из леса?
3) 34 - 16 = 18 (гр.)
Пояснение
а) В роще 240 берёз, а клёнов на 93 меньше. Вычислим, сколько клёнов в роще:
1) 240 - 93 = 147 (кл.)
В роще 147 клёнов, а сосен в ней вдвое больше. Вычислим, сколько сосен в роще:
2) 147 • 2 = 294 (с.)
В роще 294 сосны и 240 берёз. Вычислим, сколько сосен и берёз вместе:
3) 294 + 240 = 534 (д.)
В роще 534 сосен и берёз вместе, а елей - в 3 раза меньше. Вычислим, сколько елей в роще:
4) 534 : 3 = 178 (ел.)
В роще 534 сосен и берёз вместе, 178 елей и 147 клёнов. Узнаем, сколько всего деревьев в этой роще:
5) 534 + 178 + 147 = 859 (д.)
б) Из леса принесли 38 грибов: белых, подосиновиков и подберёзовиков. Из них подберёзовиков и подосиновиков вместе было 34 гриба. Вычислим, сколько белых грибов принесли из леса:
1) 38 - 34 = 4 (гр.)
Из леса принесли 4 белых гриба, подберёзовиков - в 4 раза больше. Вычислим, сколько подберёзовиков принесли из леса:
2) 4 • 4 = 16 (гр.)
Из леса принесли 34 подберёзовика и подосиновика, из них подберёзовиков - 16. Узнаем, сколько подосиновиков принесли из леса:
3) 34 - 16 = 18 (гр.)
Вопрос
Задание № 7. При делении на 96 оказалось, что частное равно 325, а остаток равен 37. Какое число делили?
Подсказка
Повтори алгоритм письменного умножения.
Ответ
Решение
325 • 96 + 37 = 31237
Пояснение
а = b • c + r, где r < b
Чтобы найти делимое, нужно частное умножить на делитель и прибавить остаток:
325 • 96 + 37 = 31237
| × | 3 | 2 | 5 | ||
| 9 | 6 | ||||
| + | 1 | 9 | 5 | 0 | |
| 2 | 9 | 2 | 5 | ||
| 3 | 1 | 2 | 0 | 0 |
Вопрос
Задание № 8. Реши уравнения с комментированием и сделай проверку:
| а) (920 - х) : 20 + 25 = 63 | б) (150 : у + 7) • 40 = 480 |
Подсказка
Ответ
Решение
|
а) (920 - х) : 20 + 25 = 63 (920 - х) : 20 = 63 - 25 (920 - х) : 20 = 38 920 - х = 38 • 20 920 - х = 760 х = 920 - 760 х = 160 Проверка: (920 - 160) : 20 + 25 = 63 760 : 20 + 25 = 63 38 + 25 = 63 63 = 63 |
б) (150 : у + 7) • 40 = 480 150 : у + 7 = 480 : 40 150 : у + 7 = 12 150 : у = 12 - 7 150 : у = 5 у = 150 : 5 у = 30 Проверка: (150 : 30 + 7) • 40 = 480 (5 + 7) • 40 = 480 12 • 40 = 480 480 = 480 |
Пояснение
Алгоритм решения уравнений, требующих упрощения записи, имеет следующий вид:
1. Найти значение числового выражения.
2. Определить неизвестный компонент действия.
3. Выбрать и применить правило его нахождения.
4. Выполнить действия.
5. При необходимости сделать проверку.
6. Назвать ответ.
Вопрос
Задание № 9. Найди множества решений двух неравенств. Что ты замечаешь?
а) а < 5 и а  5; 5; |
б) 3 > b и с < 3; | в) х > 7 и х  8. 8. |
Подсказка
Повтори, что такое неравенства.
Ответ
Решение
|
а) {0, 1, 2, 3, 4} и {0, 1, 2, 3, 4, 5} Множество решений второго неравенства, в отличие от первого, содержит число 5. |
|
б) {0, 1, 2} и {0, 1, 2} Множества решений неравенств совпадают. |
|
в) {8, 9, 10, ...} и {8, 9, 10, ...} Множества решений неравенств совпадают. |
Пояснение
Полный список решений неравенства называют множеством решений этого неравенства.
Вопрос
Задание № 10. На луче указаны некоторые числа. Запиши неравенств так, чтобы отмеченные числа были его решениями.
Существуют ли другие неравенства, удовлетворяющие этому условию? Приведи примеры.
Подсказка
Повтори, что такое неравенства.
Ответ
Вернуться к содержанию учебника