Упражнение 1148 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Расстояние - \(60\) км.

Собственная скорость - \(4\) км/ч.

Скорость - течения \(2\) км/ч.

Стоянка - \(2\) ч.

\(l(t) - ?\),

\(l\) - пройденное расстояние,

\(t\) - время в пути.

\(16+4=20\) (км/ч) - скорость катера по течению.

\(16-4=12\) (км/ч) - скорость катера против течения.

\(60 : 20 = 3\) (ч) - время в пути из \(A\) в \(B\).

\(60 : 12 = 5 \) (ч) - время в пути из \(B\) в \(A\).

\(3 + 2 + 5 = 10\) (ч) - общее время в пути.

\( l(t)= \begin{cases} 20t,  при   0\le t < 3,\\[2mm] 60,  при    3\le t \le 5,\\[2mm] 60-12\,(t-5),  при    5 < t\le 10. \end{cases} \)

\( l(t)= \begin{cases} 20t,  при   0\le t < 3,\\[2mm] 60,  при    3\le t \le 5,\\[2mm] 120-12t,  при    5< t\le 10. \end{cases} \)

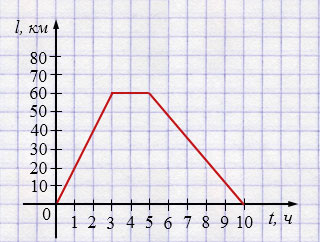
\(D(l) = [0,10]\).

\(E(l) = [0,60]\).

При \(t \in [0; 3)\) - функция возрастает, катер удаляется от пункта \(A\).

При \(t \in [3; 5]\) - функция не изменяется, катер стоит в пункте \(B\).

При \(t \in (3; 10]\) - функция убывает, катер возвращается в пункт \(A\).

Пояснения:

Использованные формулы движения:

\( s=vt,\)

\(v_{\text{по теч.}}=v_{\text{собств.}}+v_{\text{теч.}},\)

\(v_{\text{против теч.}}=v_{\text{собств.}}-v_{\text{теч.}}. \)

На участке \(0\le t\le 3\) катер идёт вниз по реке (по течению) со скоростью \(20\) км/ч, поэтому расстояние от \(A\) растёт линейно: \(l=20t\).

На участке стоянки \(3\le t\le 5\) катер находится в \(B\), расстояние от \(A\) постоянно и равно \(60\): получаем горизонтальный отрезок графика.

На обратном пути \(5\le t\le 10\) катер идёт против течения со скоростью \(12\) км/ч, расстояние до \(A\) убывает линейно: \(l=60-12(t-5)\).

В момент \(t=10\) катер возвращается в \(A\), и \(l(10)=0\).

Физический смысл: рост расстояния соответствует движению от \(A\) к \(B\), горизонтальный участок — стоянке, убывание — возвращению к \(A\).

\[ xy - 2x + 3y - 6 = 0. \]

\[ x(y - 2) + 3(y - 2) =0\]

\[(x + 3)(y - 2) = 0 \]

\(x+3 = 0\)  или  \(y - 2 = 0\)

\( x = -3\)              \(y = 2\)

Прямые \(x = -3\) и \(y = 2\) пересекаются в точке \((-3, 2)\).

Пояснения:

Основная идея: если уравнение второго порядка относительно \(x\) и \(y\) можно разложить на произведение двух линейных множителей, то его график представляет собой пару прямых.

В данном случае произведение

\((x + 3)(y - 2) = 0\) задаёт две прямые:

— первая прямая:

\(x + 3 = 0 \Rightarrow x = -3\) - вертикальная прямая.

— вторая прямая:

\(y - 2 = 0 \Rightarrow y = 2\) - горизонтальная прямая.

Полученные прямые пересекаются в точке — \((-3, 2)\). Это доказывает, что уравнение действительно задаёт пару пересекающихся прямых.