Упражнение 508 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№508 учебника 2023-2025 (стр. 114):
Постройте графики функций:
1) \(y = \sqrt{x};\)
2) \(y = \sqrt{x} - 3;\)
3) \(y = \sqrt{x} + 3;\)
4) \(y = \sqrt{x - 3};\)
5) \(y = \sqrt{x + 3}.\)
№508 учебника 2013-2022 (стр. 116):
При каком значении \(x\) дробь
\[ \frac{\sqrt{x}-\sqrt{2}}{x-2} \]
принимает наибольшее значение?
Подсказка
№508 учебника 2023-2025 (стр. 114):
Вспомните:
- Функцию \(y=\sqrt x\) и ее график.
- Координаты точки.
- Что называют арифметическим квадратным корнем.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№508 учебника 2013-2022 (стр. 116):
Вспомните:
- Освобождение от иррациональности.
- Рациональные дроби.
- Основное свойство рациональной дроби (сокращение дробей).
- Что называют арифметическим квадратным корнем.
- Свойства арифметического квадратного корня.
- Степень с натуральным показателем.
- Разность квадратов двух выражений.
Ответ
№508 учебника 2023-2025 (стр. 114):
1) \(y = \sqrt{x}\)
\(x \ge 0\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
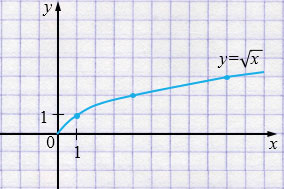
2) \(y = \sqrt{x} - 3\)
\(x \ge 0\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | -3 | -2 | -1 | 0 |
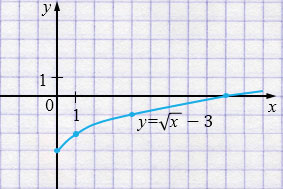
3) \(y = \sqrt{x} + 3\)
\(x \ge 0\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 3 | 4 | 5 | 6 |

4) \(y = \sqrt{x - 3}\)
\(x - 3 \ge 0\)
\(x \ge 3\)
| \(x\) | 3 | 4 | 7 | 12 |
| \(y\) | 0 | 1 | 2 | 3 |
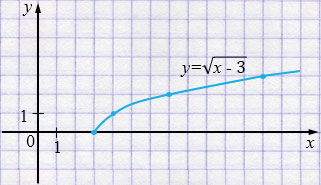
5) \(y = \sqrt{x + 3}\)
\(x + 3 \ge 0\)
\(x \ge -3\)
| \(x\) | -3 | -2 | 1 | 6 |
| \(y\) | 0 | 1 | 2 | 3 |
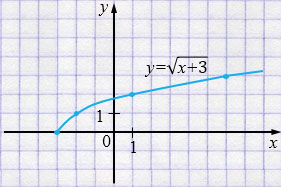
Пояснения:
При построении графиков учитываем область определения функции: корень существует только в том случае, когда подкоренное выражение неотрицательно.
В каждом случае графиком является ветвь параболы. Строим по точкам, учитывая область определения функции. Подбираем такие значения \(x\), чтобы корень можно было извлечь.
№508 учебника 2013-2022 (стр. 116):
\(\frac{\sqrt{x}-\sqrt{2}}{x-2},\quad x\ge0,\;x\ne2. \)
\(\frac{\sqrt{x}-\sqrt{2}}{x-2} =\)
\(=\frac{(\sqrt{x}-\sqrt{2})(\sqrt{x}+\sqrt{2})}{(x-2)(\sqrt{x}+\sqrt{2})} =\)
\(=\frac{(\sqrt{x})^2-(\sqrt{2})^2}{(x-2)(\sqrt{x}+\sqrt{2})} =\)
\(=\frac{\cancel{x-2}}{\cancel{(x-2)}(\sqrt{x}+\sqrt{2})} =\)
\(=\frac{1}{\sqrt{x}+\sqrt{2}}. \)
Наибольшее значение дробь принимает при \(x=0\).
Ответ: \(x=0\).
Пояснения:
1. Область определения: подкоренное выражение должно быть неотрицательным и знаменатель должен быть отличен от нуля, то есть \(x\ge0\), \(x\ne2\)
2. Умножили числитель и знаменатель на \(\sqrt{x}+\sqrt2\), чтобы избавиться от иррациональности в числителе.
Свойство корня:
\((\sqrt{x})^2 = x\).
3. Сократили одинаковый множитель в числителе и знаменателе полученной дроби:
\(\frac{ka}{kb} = \frac{a}{b}\).
4. После упрощения получили дробь \(\frac{1}{\sqrt{x}+\sqrt{2}},\) которая принимает наибольшее значение при наименьшем знаменателе, а знаменатель будет наименьшим при \(x = 0\).
Вернуться к содержанию учебника