Упражнение 328 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№328 учебника 2023-2025 (стр. 78):
Изобразите схематически в одной и той же системе координат графики функций \(y = \frac{10}{x}\) и \(y = 10x\). Имеют ли эти графики общие точки, и если имеют, то сколько?
№328 учебника 2013-2022 (стр. 80):
Найдите квадрат числа:
\(\sqrt{25};\;\sqrt{81};\;\sqrt{2};\;\sqrt{3};\;-\sqrt{4};\)
\(\sqrt{5};\;-\sqrt{6};\;\sqrt{\tfrac{1}{2}};\;\sqrt{1{,}3}.\)
Подсказка
№328 учебника 2023-2025 (стр. 78):
№328 учебника 2013-2022 (стр. 80):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
Ответ
№328 учебника 2023-2025 (стр. 78):
\(y=\frac{10}{x}\) - гипербола.
\(y=10x\) - прямая.
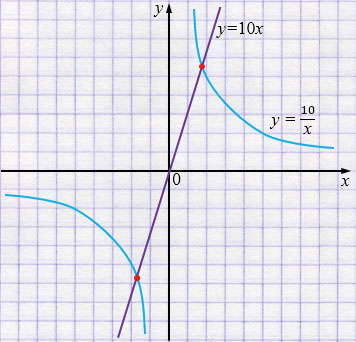
Ответ: графики имеют две общие точки.
Пояснения:
1) График \(y=10x\) — возрастающая прямая, проходящая через начало координат.
2) График \(y=\frac{10}{x}\) — гипербола, ветви которой находятся в I и III координатных четвертях.
№328 учебника 2013-2022 (стр. 80):
а) \(\bigl(\sqrt{25}\bigr)^2 = 25\).
б) \(\bigl(\sqrt{81}\bigr)^2 = 81\).
в) \(\bigl(\sqrt{2}\bigr)^2 = 2\).
г) \(\bigl(\sqrt{3}\bigr)^2 = 3\).
д) \(\bigl(-\sqrt{4}\bigr)^2 = 4\).
е) \(\bigl(\sqrt{5}\bigr)^2 = 5\).
ж) \(\bigl(-\sqrt{6}\bigr)^2 = 6\).
з) \(\bigl(\sqrt{\frac{1}{2}}\bigr)^2 = \frac{1}{2}\).
и) \(\bigl(\sqrt{1{,}3}\bigr)^2 = 1{,}3\).
Пояснения:
Использованные правила:
1) Квадрат квадратного корня:
\(\bigl(\sqrt{A}\bigr)^2 = A\) при \(A\ge0\).
2) Квадрат минус корня:
\(\bigl(-\sqrt{A}\bigr)^2 = (-1)^2\cdot\bigl(\sqrt{A}\bigr)^2 = A\).
Для всех случаев подкоренное выражение неотрицательно, поэтому можно применять правила.
Вернуться к содержанию учебника