Упражнение 1204 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1204 учебника 2023-2025 (стр. 234):
Свежие грибы содержат 90 % воды, а сухие грибы — 12 % воды. Сколько получится сухих грибов из 11 кг свежих?
№1204 учебника 2013-2022 (стр. 233):
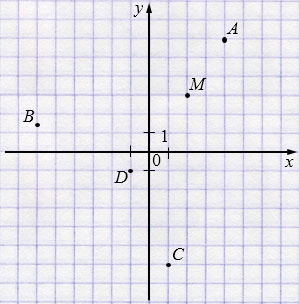
На координатной плоскости (рис. 85) отмечена точка M\((x,y)\). Отметьте в этой же координатной плоскости точки A\((2x,2y)\), B\(\bigl(-3x,\tfrac12y\bigr)\), C\(\bigl(\tfrac12x,-2y\bigr)\), D\(\bigl(-\tfrac12x,-\tfrac13y\bigr)\).
Подсказка
№1204 учебника 2023-2025 (стр. 234):
Вспомните:
- Проценты.
- Умножение десятичных дробей.
- Деление десятичных дробей.
№1204 учебника 2013-2022 (стр. 233):
Вспомните:
- Координаты точки.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Десятичная запись дробных чисел.
Ответ
№1204 учебника 2023-2025 (стр. 234):
| Вода |
Сухое вещество |
|
|
Свежие грибы |
90% = 0,9 | 10% = 0,1 |
|
Сухие грибы |
12% = 0,12 | 88% = 0,88 |
1) \( 11 \cdot 0{,}1 = 1{,}1\) (кг) - масса сухого вещества в свежих грибах, также и масса сухого вещества в сухих грибах.
2) \(1{,}1 : 0{,}88 = 110 : 88 = 1{,}25\) (кг)
| - | 1 | 1 | 0 | 8 | 8 | |||||||||||
| 8 | 8 | 1 | , | 2 | 5 | |||||||||||
| - | 2 | 2 | 0 | |||||||||||||
| 1 | 7 | 6 | ||||||||||||||
| - | 4 | 4 | 0 | |||||||||||||
| 4 | 4 | 0 | ||||||||||||||
| 0 |
Ответ: получится 1,25 кг сухих грибов.
Пояснения:
– Сухое вещество сохраняется при сушке.
– Доля сухого вещества:
в свежих — 10 %, в сухих — 88 %.
– Массу сухих грибов нашли как массу сухого вещества, делённую на долю сухого вещества в сухих.
№1204 учебника 2013-2022 (стр. 233):
M\((x; y)\)
\(x = 2\), \(y = 3\), значит, M\((2; 3)\).
A\(\bigl(2x; 2y\bigr)\)
\(2x = 2\cdot2 = 4\),
\(2y = 2\cdot3 = 6\), значит, A\((4; 6)\).
B\(\bigl(-3x; \tfrac12y\bigr)\)
\(-3x = -3\cdot2 = -6\),
\(\tfrac12y =\tfrac12\cdot3 = \tfrac32 =1,5\),
значит, B\((-6; 1,5)\).
C\(\bigl(\tfrac12x; -2y\bigr)\)
\(\tfrac12x = \tfrac12\cdot2 = 1\),
\(-2y = -2\cdot3 = -6\), значит, С\((1; -6)\).
D\(\bigl(-\tfrac12x,-\tfrac13y\bigr)\)
\(-\tfrac12x = -\tfrac12\cdot2 = -1\),
\(-\tfrac13y = -\tfrac13\cdot3 = -1\), значит, D\((-1; -1)\).
Пояснения:
1. Точка M имеет координаты \((x,y)\).
2. Координаты новых точек получаются так:
– A: умножаем обе координаты M на 2 → \(\bigl(2x,2y\bigr)\).
– B: абсциссу умножаем на –3, ординату на ½ → \(\bigl(-3x,\tfrac12y\bigr)\).
– C: абсциссу делим на 2, ординату умножаем на –2 → \(\bigl(\tfrac12x,-2y\bigr)\).
– D: абсциссу меняем знак и делим на 2, ординату меняем знак и делим на 3 → \(\bigl(-\tfrac12x,-\tfrac13y\bigr)\).
Вернуться к содержанию учебника