Упражнение 801 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№801 учебника 2023-2025 (стр. 163):
Докажите, что:
а) произведение двух средних из четырёх последовательных целых чисел на 2 больше произведения крайних чисел;
б) квадрат среднего из трёх последовательных нечётных чисел на 4 больше произведения двух крайних чисел.
№801 учебника 2013-2022 (стр. 166):
С помощью рисунка 86 разъясните геометрический смысл формулы
\[(a - b)^2 = a^2 - 2ab + b^2\]
для положительных \(a\) и \(b\), удовлетворяющих условию \(a > b\).
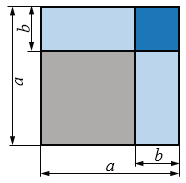
Рис.71
Подсказка
№801 учебника 2023-2025 (стр. 163):
Вспомните:
- Целые числа.
- Умножение одночлена на многочлен.
- Умножение многочлена на многочлен.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Степень с натуральным показателем
№801 учебника 2013-2022 (стр. 166):
Вспомните:
- Как найти площадь квадрата.
- Как найти площадь прямоугольника.
- Формула квадрата разности двух выражений.
Ответ
№801 учебника 2023-2025 (стр. 163):
а) Пусть четыре последовательных целых числа:
\(x,\;x+1,\;x+2,\;x+3\).
\( (x+1)(x+2)\;-\;x(x+3) =\)
\(=\cancel{x^2} + \cancel{3x}+2 - \cancel{x^2} - \cancel{3x}=2. \)
б) Пусть три последовательных нечётных числа:
\( 2x+1,\;2x+3,\;2x+5\).
\( (2x+3)^2-(2x+1)(2x+5)= \)
\( (2x+3)(2x+3) - (2x+1)(2x+5)= \)
\(=(4x^2+6x+6x+9) -(4x^2+10x+2x+5) =\)
\(=(4x^2+12x+9) -(4x^2+12x+5) =\)
\(=\cancel{4x^2}+\cancel{12x}+9 - \cancel{4x^2}-\cancel{12x}-5 =\)
\(=9 - 5 = 4.\)
Пояснения:
1. Метод «через разность» состоит в сравнении выражений путём вычитания: выясняем, на какое число одно выражение больше другого.
2. Раскрываем скобки по правилам:
• умножения многочлена на многочлен:
\((a+b)(c+d) = ac+ad+bc+bd\);
• умножения одночлена на многочлен:
\(a(b+c)=ab+ac\).
3. В пункте (а) после раскрытия скобок сокращаются члены \(x^2\) и \(3x\), остаётся 2.
4. В пункте (б) сначала представляем квадрат среднего числа в виде произведения двух одинаковых скобок по определению степени, после раскрытия скобок сокращаются члены \(x^2\) и \(4x\), остаётся 4.
5. Полученные равенства доказывают:
а) произведение средних чисел больше произведения крайних на 2;
б) квадрат среднего нечётного на 4 больше произведения двух крайних чисел.
№801 учебника 2013-2022 (стр. 166):
1) Сторона серого квадрата равна
\(a - b\), его площадь равна\((a - b)^2.\)
2) Площадь квадрата со стороной \(a\) равна \(a^2.\)
Площадь прямоугольника со сторонами \(a\) и \(b\) равна \(a\cdot{b}\), тогда площадь двух таких прямоугольников равна \(2ab\)
Площадь квадрата со стороной \(b\) равна \(b^2.\) Тогда площадь серого квадрата:
\(a^2 - 2ab + b^2.\)
3) \((a - b)^2 = a^2 - 2ab + b^2.\)
Пояснения:
– Рисунок 86 иллюстрирует разбиение большого квадрата на четыре фигуры: квадрат со стороной \(a - b\), два равных прямоугольника \(a\times b\) и малый квадрат со стороной \(b\).
– Площадь большого квадрата — сумма площадей всех этих частей. Вычитая из \(a^2\) площади двух прямоугольников \(2ab\) и малого квадрата \(b^2\), получаем площадь оставшегося квадрата \((a - b)^2\).
– Это наглядно демонстрирует формулу квадрата разности через площади фигур.
Вернуться к содержанию учебника