Упражнение 760 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 158
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№760 учебника 2023-2025 (стр. 158):
Докажите, что:
а) сумма чисел \(\overline{ab}\) и \(\overline{ba}\) кратна сумме \(a\) и \(b\);
б) разность чисел \(\overline{ab}\) и \(\overline{ba}\) кратна 9.
№760 учебника 2013-2022 (стр. 158):
Из A в B одновременно выехали два мотоциклиста. Скорость одного из них в 1,5 раза больше скорости другого. Мотоциклист, который первым прибыл в B, сразу же отправился обратно. Другого мотоциклиста он встретил через 2 ч 24 мин после выезда из A. Расстояние между A и B равно 120 км. Найдите скорости мотоциклистов и расстояние от места встречи до B.
Подсказка
№760 учебника 2023-2025 (стр. 158):
Вспомните:
- Что называют многочленом.
- Запись многозначного числа в виде многочлена.
- Разряды многозначных чисел.
- Подобные слагаемые, раскрытие скобок.
- Свойства делимости.
№760 учебника 2013-2022 (стр. 158):
Вспомните:
- Решение задач с помощью уравнений.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Задачи на движение.
- Умножение десятичных дробей.
- Сложение десятичных дробей.
- Сокращение дробей.
- Единицы измерения времени.
Ответ
№760 учебника 2023-2025 (стр. 158):
\[ \overline{ab} = 10a + b,\quad \overline{ba} = 10b + a. \]
а) \( \overline{ab} + \overline{ba} =\)
\(=(10a + b) + (10b + a) =\)
\(=10a + b + 10b + a =\)
\(=11a + 11b = 11\,(a + b) \) - кратно сумме \(a+b\).
б) \( \overline{ab} - \overline{ba} =\)
\(=(10a + b) - (10b + a) =\)
\(=10a + b - 10b - a =\)
\(=9a - 9b = 9\,(a - b). \) - кратно 9.
Пояснения:
1. Десятичная запись. Число \(\overline{ab}\) в виде многочлена равно \(10a + b\),
где \(a\) — количество десятков,
\(b\) — количество единиц.
2. Делимость на сумму цифр. Выражение \(11(a+b)\) содержит множитель \((a+b)\), поэтому делится на него без остатка.
3. Делимость на 9. Произведение \(9\,(a-b)\) содержит множитель 9, значит, разность чисел делится на 9.
№760 учебника 2013-2022 (стр. 158):
1) \(2 \text{ч } 24 \text{ мин} =2\frac{\cancel{24}^2}{\cancel{60}^5}\text{ ч}=2\frac{2}{5}\text{ ч}=2,4\text{ ч}\)
2) \(120 \cdot 2 = 240 \text{ (км)}\) - вместе проехали первый и второй мотоциклисты.
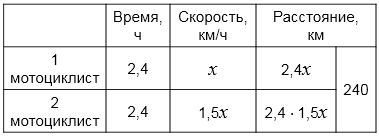
3) Составим уравнение:
а) \(2{,}4\cdot1{,}5x + 2{,}4x = 240\)
| × | 2 | 4 | |
| 1 | 5 | ||
| + | 1 | 2 | 0 |
| 2 | 4 | ||
| 3 | 6 | 0 |
\(3,6x + 2{,}4x = 240\)
\(6x = 240\)
\(x = \frac{240}{6}\)
\(x = 40 \text{ (км/ч)}\) - скорость первого мотоциклиста.
4) \(1{,}5x = 1{,}5 \cdot 40 = 60 \text{ (км/ч)}\) - скорость второго мотоциклиста.
б) \(120 - 2,4\cdot40 = 120 - 96 = \)
\(=24 \text{ (км)}\) - расстояние от места встречи до B.
Ответ: 40 км/ч, 60 км/ч, 24 км.
Пояснения:
Использованные формулы и обозначения:
\(x\) — скорость первого (медленного) мотоциклиста;
\(1{,}5x\) — скорость второго (быстрого) мотоциклиста;
\(s = vt\) — путь равен произведению скорости на время.
1. За время \(t = 2{,}4\) ч (т.е. 2 ч 24 мин) первый проехал от A до точки встречи путь
\[x \cdot 2{,}4 = 2{,}4x.\]
2. Второй за это же время прошёл путь
\[1{,}5x \cdot 2{,}4 = 3{,}6x,\]
из которых первые 120 км — от A до B, а оставшиеся — от B до места встречи, то есть получается, что вместе мотоциклисты проехали
\(120 \cdot 2 = 240 \text{ (км)}\), поэтому составляем следующее уравнение:
\(3{,}6x + 2{,}4x = 240\), откуда
\(6x = 240\) и получаем, что скорость первого мотоциклиста:
\(x = 40 \text{ (км/ч)}\).
Значит, скорость второго мотоциклиста:
\(1{,}5x = 1{,}5 \cdot 40 = 60 \text{ (км/ч)}\)
Расстояние до встречи - это расстояние, которое первый велосипедист не доехал до пункта В, тогда, учитывая то что расстояние между пунктами А и В равно 120 км, расстояние от места встречи до B равно:
\(120 - 2,4\cdot40 = 120 - 96 =\)
\(=24 \text{ (км)}\).
Вернуться к содержанию учебника