Упражнение 568 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№568 учебника 2023-2025 (стр. 127):
Докажите, что при любом натуральном k:
а) число 34k оканчивается единицей;
б) число 10k - 1 кратно 3.
№568 учебника 2013-2022 (стр. 128):
Приведите подобные члены многочлена:
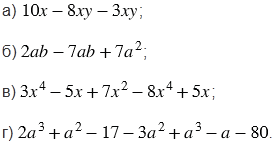
Подсказка
№568 учебника 2023-2025 (стр. 127):
Вспомните:
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Кратные числа.
№568 учебника 2013-2022 (стр. 128):
Вспомните:
- Одночлены.
- Многочлены.
- Пподобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№568 учебника 2023-2025 (стр. 127):
а) 34k = (34)k = 81k - при любом значении k оканчивается единицей. Что и требовалось доказать.
б) Число 10k состоит из единицы и k нулей, значит, число 10k - 1 будет состоять из k девяток (10 - 1 = 9, 100 - 1 = 99, 1000 - 1 = 999 и т.д.), а число, состоящее из любого количества девяток делится нацело на 9, следовательно, число 10k - 1 при любом значении k кратно 3. Что и требовалось доказать.
№568 учебника 2013-2022 (стр. 128):

Пояснения:
Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене - приведением подобных членов многочлена.
Подобные слагаемые - это слагаемые, которые имеют одинаковую буквенную часть, т.е. подобные слагаемые могут отличаться только коэффициентами (в решении подобные слагаемые выделены одинаковым цветом). Чтобы сложить (или привести) подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
Вернуться к содержанию учебника