Упражнение 374 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№374 учебника 2023-2025 (стр. 92):
Скорость распространения звука в воздухе в зависимости от температуры воздуха может быть найдена приближенно по формуле 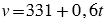 , где
, где 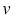 - скорость (в метрах в секунду),
- скорость (в метрах в секунду), 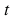 - температура (в градусах Цельсия). Найдите, с какой скоростью распространяется звук в зимний день с температурой -35 0С и летний день с температурой +30 0С.
- температура (в градусах Цельсия). Найдите, с какой скоростью распространяется звук в зимний день с температурой -35 0С и летний день с температурой +30 0С.
№374 учебника 2013-2022 (стр. 95):
Запишите произведение в виде степени:
а) \(0,9 \cdot 0,9 \cdot 0,9\);
б) \((-6)\cdot(-6)\cdot(-6)\cdot(-6)\);
в) \(\tfrac12\cdot\tfrac12\cdot\tfrac12\cdot\tfrac12\);
г) \(\underset{25\text{ раз}}{\underbrace{5\cdot 5\cdot ...\cdot 5 }}\);
д) \(ccccccc\);
е) \(\underset{12\text{ раз}}{\underbrace{yy ...y}}\);
ж) \((-x)\cdot(-x)\cdot(-x)\cdot(-x)\cdot(-x)\);
з) \((a - b)(a - b)\);
и) \((xy)(xy)(xy)(xy)(xy)\).
Подсказка
№374 учебника 2023-2025 (стр. 92):
Вспомните:
- Связи между величинами.
- Способы задания функции.
- Порядок выполнения действий.
- Умножение десятичных дробей.
- Умножение рациональных чисел.
№374 учебника 2013-2022 (стр. 95):
Вспомните степень с натуральным показателем.
Ответ
№374 учебника 2023-2025 (стр. 92):

№374 учебника 2013-2022 (стр. 95):
а) \(0,9 \cdot 0,9 \cdot 0,9 = 0,9^3\);
б) \((-6)\cdot(-6)\cdot(-6)\cdot(-6)=\bigl(-6\bigr)^4\);
в) \(\tfrac12\cdot\tfrac12\cdot\tfrac12\cdot\tfrac12=\bigl(\tfrac12\bigr)^4\);
г) \(\underset{25\text{ раз}}{\underbrace{5\cdot 5\cdot ...\cdot 5 }}=5^{25}\);
д) \(ccccccc=c^7\);
е) \(\underset{12\text{ раз}}{\underbrace{yy ...y}}=y^{12}\);
ж) \((-x)\cdot(-x)\cdot(-x)\cdot(-x)\cdot(-x)=\bigl(-x\bigr)^5\);
з) \((a - b)(a - b)=(a - b)^2\);
и) \((xy)(xy)(xy)(xy)(xy)=(xy)^5\).
Пояснения:
Основное правило для сокращения повторяющегося произведения:
\[\underbrace{a\cdot a\cdots a}_{n\text{ раз}} = a^n.\]
В каждом пункте мы просто определяем, сколько раз повторяется один и тот же множитель, и записываем результат в виде степени.
— а) множитель \(0,9\) повторяется 3 раза, тогда имеем \((0,9)^3\).
— б) множитель \(-6\) повторяется 4 раза, тогда имеем \((-6)^4\).
— в) множитель \(\tfrac12\) повторяется 4 раза, тогда имеем \(\bigl(\tfrac12\bigr)^4\).
— г) множитель \(5\) повторяется 25 раз, тогда имеем \(5^{25}\).
— д) множитель \(c\) повторяется 7 раз, тогда имеем \(c^7\).
— е) множитель \(y\) повторяется 12 раз, тогда имеем \(y^{12}\).
— ж) множитель \(-x\) повторяется 5 раз, тогда имеем \(\bigl(-x\bigr)^5\).
— з) множитель \((a - b)\) повторяется 2 раза ⇒ \((a - b)^2\).
— и) множитель \((xy)\) повторяется 5 раз ⇒ \((xy)^5\).
Вернуться к содержанию учебника