Задание 6.382 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2. Страница 128

Пусть скорость лыжника на первом участке трассы 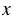км/ч.

1) 3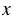 (км) - первый участок трассы.

2) 25 • 2 = 50 (км) - второй участок трассы.

3) 3 + 2 = 5 (ч) - общее время в пути.

4) 28 • 5 = 140 (км) - весь пройденный путь.

5) Составим уравнение:

3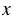 + 50 = 140

3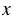 = 140 - 50

3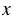 = 90

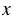= 90 : 3

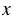= 30

30 км/ч - скорость лыжника на первом участке трассы.

Ответ: 30 км/ч.

Пояснения:

Решаем задачу с помощью уравнения.

Чтобы найти расстояние (пройденный путь), нужно скорость движения умножить на время в пути.

Пусть 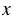км/ч - скорость лыжника на первом участке трассы, тогда за 3 ч на первом участке трассы лыжник прошел 3 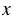(км).

На втором участке трассы лыжник шел 2 ч со скоростью 25 км/ч, значит, второй участок трассы равен:

25 • 2 = 50 (км).

Всю трассу лыжник прошел за:

3 + 2 = 5 (ч).

Чтобы найти среднюю скорость движения, нужно весь пройденный путь разделить на все время движения. Тога, если умножить среднюю скорость движения на все время в пути, получим весь пройденный путь.

Средняя скорость лыжника 28 км/ч, а все время в пути - 5 ч, значит, весь пройденный лыжником путь (длина трассы) равен:

28 • 5 = 140 (км).

Итак, первый участок трассы - 3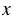 км, второй - 50 км, длина всей трассы равна 140 км, значит, можем составить следующее уравнение:

3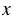 + 50 = 140.

Сначала решаем уравнение относительно сложения, в котором неизвестно первое слагаемое. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:

3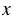 = 140 - 50,

3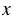 = 90.

Теперь находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда

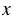= 90 : 3,

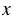= 30.

Учитывая обозначения введенные выше, скорость лыжника на первом участке трассы равна 30 км/ч.