Задание 6.366 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.366 учебника 2023-2024 (стр. 141):
Из одного поселка в противоположных направлениях отправились велосипедист и пешеход. Скорость пешехода в 3,5 раза меньше скорости велосипедиста. Найдите их скорости, если за 0,6 ч они удалились друг от друга на 11,61 км.
№6.366 учебника 2021-2022 (стр. 125):
Найдите значение выражения:
а) 4,292 : (9 - 5,3) + 2,6 • (1,89 + 1,51);
б)(5,4:2,7 + 0,96:2,4)•2,4 + 0,046:1,15;
в) (5,04 : 4,2 - 0,78 : 3,9) : 0,125 - 3,6;
г) 11,96 : 9,2 • 1,8 - 0,42 • 4,2 : 8,4.
Подсказка
№6.366 учебника 2023-2024 (стр. 141):
Вспомните:
- Задачи на движение.
- Что называют уравнением, его корни.
- Деление десятичных дробей.
- Умножение десятичных дробей (распределительное свойство).
- Сложение десятичных дробей.
№6.366 учебника 2021-2022 (стр. 125):
Вспомните:
- Порядок выполнения действий.
- Сложение и вычитание десятичных дробей.
- Умножение десятичных дробей.
- Деление десятичных дробей.
Ответ
№6.366 учебника 2023-2024 (стр. 141):
1) 11,61 : 0,6 = 116,1 : 6 = 19,35 (км/ч) - скорость удаления.
| - | 1 | 1 | 6 | 1 | 6 | |||||||||||||
| 6 | 1 | 9 | 3 | 5 | ||||||||||||||
| - | 5 | 6 | ||||||||||||||||
| 5 | 4 | |||||||||||||||||
| - | 2 | 1 | ||||||||||||||||
| 1 | 8 | |||||||||||||||||
| - | 3 | 0 | ||||||||||||||||
| 3 | 0 | |||||||||||||||||
| 0 |
2) Пусть скорость пешехода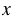 
км/ч, тогда скорость велосипедиста равна 3,5 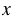км/ч. Известно, что скорость удаления 19,35 км/ч.
Составим уравнение:
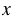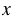+ 3,5 = 19,35
4,5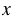 = 19,35
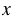= 19,35 : 4,5
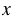= 193,5 : 45
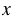= 4,3
| - | 1 | 9 | 3 | 5 | 4 | 5 | ||||||||||
| 1 | 8 | 0 | 4 | 3 | ||||||||||||
| - | 1 | 3 | 5 | |||||||||||||
| 1 | 3 | 5 | ||||||||||||||
| 0 |
4,3 км/ч - скорость пешехода.
3) 4,3 • 3,5 = 15,05 (км/ч) - скорость велосипедиста.
| × | 4 | 3 | ||
| 3 | 5 | |||
| + | 2 | 1 | 5 | |
| 1 | 2 | 9 | ||
| 1 | 5 | 0 | 5 |
Ответ: 4,3 км/ч и 15,05 км/ч.
Пояснения:
Чтобы найти скорость, нужно расстояние разделить на время.
Из одного поселка в противоположных направлениях отправились велосипедист и пешеход. За 0,6 ч они удалились друг от друга на 11,61 км. Значит, скорость их удаления:
11,61 : 0,6 = 116,1 : 6 = 19,35 (км/ч).
Далее решаем задачу с помощью уравнения.
Пусть 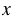км/ч скорость пешехода. Скорость велосипедиста в 3,5 раза больше скорости пешехода, тогда скорость велосипедиста 3,5 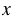км/ч. Мы установили, что скорость удаления велосипедиста и пешехода 19,35 км/ч. Получается, мы можем составить следующее уравнение:
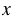+ 3,5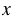 = 19,35.
Сначала в левой части полученного уравнения применяем распределительное свойство умножения относительно сложения (выносим 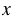за скобки), получим:
(1 + 3,5)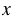 = 19,35,
4,5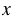 = 19,35.
Теперь находим неизвестный множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
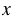= 19,35 : 4,5,
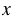= 193,5 : 45,
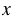= 4,3.
Учитывая обозначения введенные выше, скорость пешехода 4,3 км/ч.
Скорость велосипедиста в 3,5 раза больше скорости пешехода, то есть скорость велосипедиста равна:
4,3 • 3,5 = 15,05 (км/ч).
Правила вычислений с десятичными дробями смотрите в подсказке.
№6.366 учебника 2021-2022 (стр. 125):
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
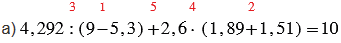
1) 5,4 : 2,7 = 2 2) 0,96 : 2,4 = 0,4 3) 2 + 0,4 = 2,4 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
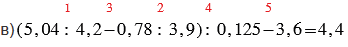
| 3) 1,2 - 0,2 = 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
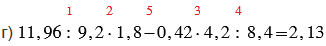
| 5) 2,34 - 0,21 = 2,13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пояснения:
Действиями первой ступени называют сложение и вычитание чисел, а действиями второй ступени - умножение и деление чисел.
При вычислении значений выражений порядок выполнения действий определяют следующие правила:
1. Если выражение содержит только действия одной ступени и в нем нет скобок, то действия выполняют по порядку слева направо.
2. Если в выражении нет скобок, то сначала выполняют действия второй ступени, потом - действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая правила 1 и 2).
Красные числа, стоящие сверху над действиями, показывают в каком порядке нужно выполнять действия.
Вернуться к содержанию учебника