стр. 125. Проверьте себя - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Проверьте себя
Вопрос
Проверочная работа №1
Деление на десятичную дробь
Найдите частное:
1. Нуля целых восьми сотых и нуля целых четырех десятых.
2. Семи целых двух десятых и нуля целых девяти десятых.
3. Одной целой пяти десятых и нуля целых пяти сотых.
4. Нуля целых восемнадцати тысячных и нуля целых трех сотых.
5. Пяти целых четырех десятых и нуля целых одной десятой.
Верно ли высказывание (ответьте да или нет)?
6. При делении числа на десятичную дробь сначала надо перенести запятую вправо в делимом и делителе на столько цифр, сколько их после запятой в делимом, а затем выполнить деление.
7. При делении числа на ноль целых одну сотую оно уменьшается.
8. Корень уравнения 3,46 : 
= 34,6 - число ноль целых одна десятая.
Вопрос
Практическая работа №2
Деление на десятичную дробь
Найдите частное:
1. Двадцати восьми и нуля целых одной десятой.
2. Пяти целых пятидесяти пяти сотых и нуля целых одной сотой.
3. Нуля целых шестидесяти четырех сотых и нуля целых восьми десятых.
4. Нуля целых пятнадцати тысячных и нуля целых пяти сотых.
5. Путь от дома до озера равен четырем километрам. Этот путь Дима проехал на велосипеде за ноль целых четыре десятых часа. С какой скоростью ехал Дима?
6. Туристы, двигаясь со скоростью четыре целых пять десятых километра в час, прошли девять километров. Сколько времени они были в пути?
Верно ли высказывание (ответьте да или нет)?
7*. При делении числа на ноль целых тридцать одну сотую число увеличивается.
8. Корень уравнения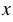 
: 0,1 = 23,5 - число двести тридцать пять.
Подсказка
Вспомните:
- Деление на десятичную дробь.
- Что называют уравнением, его корни.
- Задачи на движение.
- Сравнение десятичных дробей.
Ответ
стр. 125 учебника 2021-2022:
Проверочная работа №1
Деление на десятичную дробь
1. 0,08 : 0,4 = 0,8 : 4 = 0,2.
2. 7,2 : 0,9 = 72 : 9 = 8.
3. 1,5 : 0,05 = 150 : 5 = 30.
4. 0,018 : 0,03 = 1,8 : 3 = 0,6.
5. 5,4 : 0,1 = 54.
6. Нет.
7. 0,01 < 1, поэтому число увеличится.
Ответ: Нет.
8. 3,46 :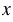 
= 34,6
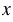= 0,1
3,46 : 0,1 = 34,6
34,6 = 34,6 - верно.
Ответ: Да.
Пояснения:
Чтобы разделить десятичную дробь на десятичную, нужно:
1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число, а именно: разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части.
Чтобы разделить десятичную дробь на 0,1, надо в этой дроби перенести запятую вправо на одну цифру.
Если при переносе запятой у делимого не хватает знаков, то помним, если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.
Число увеличивается при делении его на десятичную дробь, которая меньше единицы (задание 7).
Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство (задание 8).
стр. 125 учебника 2021-2022:
Практическая работа №2
Деление на десятичную дробь
1. 28 : 0,1 = 280.
2. 5,55 : 0,01 = 555.
3. 0,64 : 0,8 = 6,4 : 8 = 0,8.
4. 0,015 : 0,05 = 1,5 : 5 = 0,3.
5. Путь - 4 км,
время - 0,4 ч,
скорость - ? км/ч.
4 : 0,4 = 40 : 4 = 10 (км/ч)
Ответ: Дима ехал со скоростью 10 км/ч.
6. Скорость - 4,5 км/ч,
путь - 9 км,
время - ? ч.
9 : 4,5 = 90 : 45 = 2 (ч)
Ответ: туристы были в пути 2 ч.
7*. 0,31 < 1, поэтому число увеличится.
Ответ: Нет.
8. 
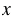: 0,1 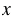= 23,5
= 235
235 : 0,1 = 23,5
2350 = 23,5 - неверно.
Ответ: нет.
Пояснения:
Чтобы разделить десятичную дробь на десятичную, нужно:
1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число, а именно: разделить дробь на это число, не обращая внимания на запятую; поставить в частном запятую, когда кончится деление целой части.
Чтобы разделить десятичную дробь на 0,1, 0,01, 0,001 и т. д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т. д. цифры.
Если при переносе запятой у делимого не хватает знаков, то помним, если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной (у натурального числа запятую подразумеваем на конце справа).
Чтобы найти скорость, нужно расстояние (путь) разделить на время (задание 5).
Чтобы найти время, нужно расстояние (путь) разделить на скорость (задание 6).
Число увеличивается при делении его на десятичную дробь, которая меньше единицы (задание 7).
Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство (задание 8).
Вернуться к содержанию учебника