Задание 6.240 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№6.240 учебника 2023-2024 (стр. 127):
Вычислите:
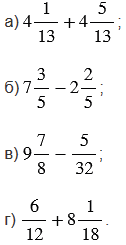
№6.240 учебника 2021-2022 (стр. 111):
Сравните выражения:
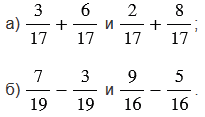
Подсказка
№6.240 учебника 2023-2024 (стр. 127):
Вспомните:
- Смешанные числа, действия с ними.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Основное свойство дроби (сокращение дробей).
- Наименьшее общее кратное.
№6.240 учебника 2021-2022 (стр. 111):
Вспомните:
- Обыкновенные дроби.
- Сравнение дробей.
- Сложение и вычитание дробей с одинаковыми знаменателями.
Ответ
№6.240 учебника 2023-2024 (стр. 127):
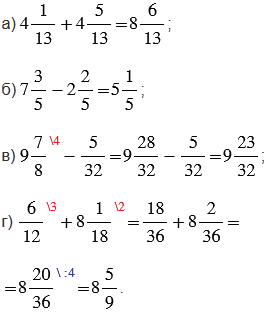
Пояснения:
При выполнении вычислений помним следующие правила:
1) чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним;
2) чтобы сложить (вычесть) две дроби с разными знаменателями, надо: привести данные дроби к наименьшему общему знаменателю (наименьшему общему кратному знаменателей складываемых дробей); применить правило сложения (вычитания) дробей с одинаковыми знаменателями (в решении красным цветом выделены дополнительные множители);
3) чтобы выполнить сложение или вычитание смешанных чисел, нужно: привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение или вычитание целых частей и отдельно дробных частей.
Также, если при вычислениях получается сократимая дробь, ее нужно сократить, то есть разделить ее числитель и знаменатель на их наибольший общий делитель (в решении число, на которое сокращаем дробь, выделено синим цветом).
№6.240 учебника 2021-2022 (стр. 111):
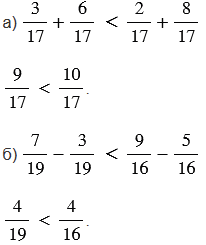
Пояснения:
а) Чтобы сравнить выражения находим их значения, выполнив сложение. Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
При сравнении помним, из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше.
б) Чтобы сравнить выражения находим их значения, выполнив вычитание. Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
При сравнении помним, из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, а меньше та, у которой знаменатель больше.
Вернуться к содержанию учебника