Задание 2.129 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.129 учебника 2023-2024 (стр. 61):
Можно ли дроби 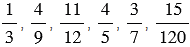 привести к знаменателю 48?
привести к знаменателю 48?
№2.129 учебника 2021-2022 (стр. 52):
За конкурс "Музыкальное приветствие" команды КВН получили следующие оценки:
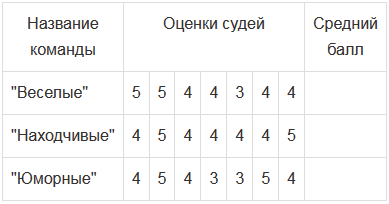
Расположите команды по возрастанию их средних баллов.
Подсказка
№2.129 учебника 2023-2024 (стр. 61):
Вспомните:
- Обыкновенные дроби.
- Основное свойство дроби.
- Наибольший общий делитель.
- Умножение чисел.
- Деление чисел.
- Приведение дробей к новому знаменателю.
№2.129 учебника 2021-2022 (стр. 52):
Вспомните:
- Как найти среднее арифметическое ряда чисел.
- Сравнение смешанных чисел.
- Сравнение обыкновенных дробей.
- Деление и дроби.
- Неправильные дроби.
- Сложение чисел.
Ответ
№2.129 учебника 2023-2024 (стр. 61):

Пояснения:
Дробь можно привести к данному знаменателю, если данный знаменатель можно разделить на знаменатель данной дроби, причем, если исходную дробь можно сократить, то дробь сначала сокращаем, а затем пробуем разделить нужный нам знаменатель на знаменатель сокращенной дроби. Если же нужный нам знаменатель не делится на знаменатель дроби, то дробь к этому знаменателю привести нельзя.
Сократить дробь, значит, разделить числитель и знаменатель дроби на их наибольший общий делитель.
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Если из двух чисел большее число делится на меньшее, то наибольшим общим делителем этих двух чисел будет меньшее число чисел.
Чтобы получить дробь с нужным знаменателем, нужно умножить числитель и знаменатель дроби на дополнительный множитель, который получается в результате деления нужного нам знаменателя на знаменатель дроби.
№2.129 учебника 2021-2022 (стр. 52):

Ответ: расположение команд по возрастанию их средних баллов: "Юморные", "Веселые", "Находчивые".
Пояснения:
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на количество слагаемых. При этом учитываем то, что деление можно записать дробью, в которой делимое - числитель, делитель - знаменатель.
В результате вычислений получаются неправильные дроби, которые нужно преобразовать в смешанные числа.
Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
При сравнении чисел учитываем то, что смешанные числа, у которых одинаковые целые части, сравниваем по дробным частям, при этом помним из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Вернуться к содержанию учебника