Задание 1.102 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1.102 учебника 2023-2024 (стр. 29):
Магнитный железняк содержит 0,7 чистого железа. Постройте круговую диаграмму распределения железа и пустой руды в магнитном железняке.
№1.102 учебника 2021-2022 (стр. 25):
Нарисуйте пятиугольник, измерьте транспортиром его углы и сложите результаты измерения.
Подсказка
№1.102 учебника 2023-2024 (стр. 29):
Вспомните:
- Представление числовой информации в круговых диаграммах.
- Окружность, круг.
- Что называют углом.
- Градусная мера угла.
- Как найти дробь от числа.
- Умножение десятичных дробей.
- Вычитание чисел.
№1.102 учебника 2021-2022 (стр. 25):
Вспомните:
- Что называют пятиугольником.
- Что называют углом.
- Градусная мера угла.
- Сложение чисел.
Ответ
№1.102 учебника 2023-2024 (стр. 29):
1) 0,7 • 3600 = 2520 - железо.
| × | 3 | 6 | 0 |
| 0 | 7 | ||
| 2 | 5 | 2 | 0 |
2) 3600 - 252 = 1080 - пустая порода.
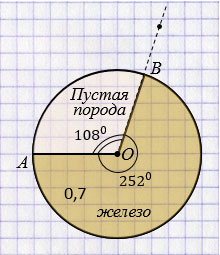
Пояснения:
В круге 3600. Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Магнитный железняк содержит 0,7 чистого железа, значит, на круговой диаграмме железо будет составлять 0,7 круга, то есть 0,7 от 3600:
0,7 • 3600 = 2520.
Остальная часть руды - пустая порода, значит, на круговой диаграмме пустая часть руды будет составлять:
3600 - 252 = 1080.
Чтобы построить круговую диаграмму, чертим круг с центром О и проводим в нем радиус ОА.

Для того чтобы начертить угол с заданной градусной мерой, необходимо совместить начало луча, который определяет одну из сторон угла, с центром транспортира, так, чтобы этот луч прошел через нулевое деление шкалы транспортира, найти на шкале транспортира нужную градусную меру и провести через это значение вторую сторону угла.
Построим  АОВ = 1080. Прикладываем центр транспортира к точке О так, чтобы радиус ОА прошел через нулевое деление на внешней шкале транспортира. Находим на внешней шкале транспортира значение 1080, ставим напротив него точку.
АОВ = 1080. Прикладываем центр транспортира к точке О так, чтобы радиус ОА прошел через нулевое деление на внешней шкале транспортира. Находим на внешней шкале транспортира значение 1080, ставим напротив него точку.

Чертим луч с началом в точке О, который пройдет через отмеченную точку, получаем
 АОВ = 1080.
АОВ = 1080.
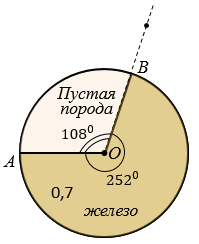
Мы построили круговую диаграмму распределения железа и пустой руды в магнитном железняке.
№1.102 учебника 2021-2022 (стр. 25):
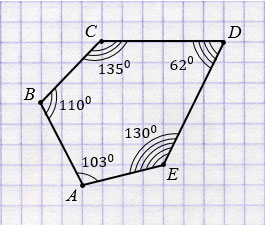
АВСDЕ - пятиугольник.
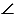 А = 1030,
А = 1030, 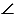 В = 1100,
В = 1100, 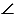 С = 1350,
С = 1350,
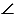 D = 620,
D = 620, 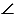 Е = 1300.
Е = 1300.
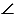 А +
А + 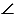 В +
В + 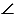 С +
С + 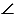 D +
D + 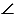 Е =
Е =
= 1030 + 1100 + 1350 + 620 + 1300 =
= 2130 + 1970 + 1300 =
= 4100 + 1300 = 5400.
Ответ: сумма углов пятиугольника равна 5400.
Пояснения:
Для того чтобы измерить угол с помощью транспортира, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы транспортира (внутренней или внешней), тогда вторая сторона угла укажет градусную меру угла (на той шкале, через нулевое деление которой проходит первая сторона).
Чертим пятиугольник АВСD.
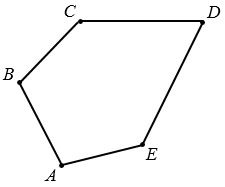
Измерим угол А пятиугольника АВСDЕ. Для этого совместим вершину угла А с центром транспортира так, чтобы сторона АЕ проходила через нулевое деление внутренней шкалы транспортира.

Сторона АВ угла А на внутренней шкале транспортира проходит через деление 1030, значит, 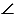 А = 1030.
А = 1030.
По такому же алгоритму измеряем остальные углы пятиугольника АВСDЕ, получаем: 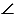 В = 1100,
В = 1100, 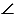 С = 1350,
С = 1350,
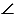 D = 620,
D = 620, 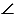 Е = 1300.
Е = 1300.
Тогда сумма углов пятиугольника АВСDЕ:
 А +
А +  В +
В + 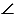 С +
С + 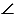 D +
D + 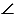 Е =
Е =
= 1030 + 1100 + 1350 + 620 + 1300=5400.
Обратите внимание, у вас может получиться пятиугольник, у которого градусные меры углов будут другими, но в сумме вы должны получить 5400.
Вернуться к содержанию учебника